Haskell Crash Course Part I

From the Lambda Calculus to Haskell














Programming in Haskell

Computation by Calculation


Substituting equals by equals













Computation via Substituting Equals by Equals









Computation via Substituting Equals by Equals

Equality-Substitution enables Abstraction via Pattern Recognition











Abstraction via Pattern Recognition

Repeated Expressions

Recognize Pattern as λ-function

Equivalent Haskell Definition

Function Call is Pattern Instance

Key Idea: Computation is substitute equals by equals.











Programming in Haskell

Substitute Equals by Equals



Thats it! (Do not think of registers, stacks, frames etc.)








Elements of Haskell

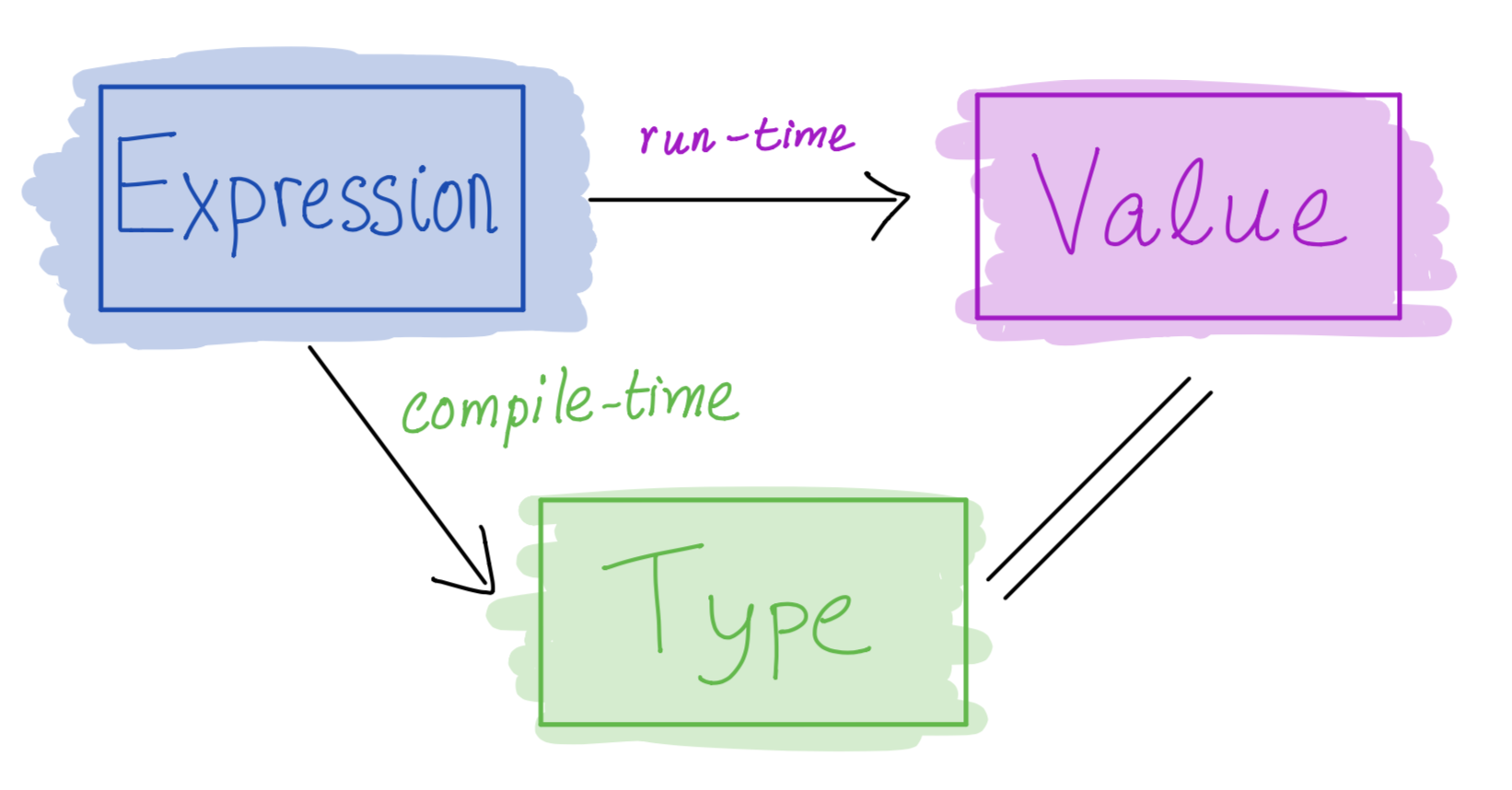
  • Core program element is an expression
  • Every valid expression has a type (determined at compile-time)
  • Every valid expression reduces to a value (computed at run-time)

Ill-typed* expressions are rejected at compile-time before execution

  • like in Java
  • not like λ-calculus or Python …









The Haskell Eco-System

  • Batch compiler: ghc Compile and run large programs

  • Interactive Shell ghci Shell to interactively run small programs online

  • Build Tool stack Build tool to manage libraries etc.









Interactive Shell: ghci









A Haskell Source File

A sequence of top-level definitions x1, x2, …

  • Each has type type_1, type_2, …

  • Each defined by expression expr_1, expr_2, …









Basic Types









QUIZ: Basic Operations

What is the type of quiz?

A. Int

B. Bool

C. Error!









QUIZ: Basic Operations

What is the value of quiz?

A. 9

B. 20

C. Other!









Function Types

In Haskell, a function is a value that has a type

A function that

  • takes input of type A
  • returns output of type B

For example

Define function-expressions using \ like in λ-calculus!

But Haskell also allows us to put the parameter on the left

(Meaning is identical to above definition with \n -> ...)









Multiple Argument Functions

A function that

  • takes three inputs A1, A2 and A3
  • returns one output B has the type

For example

which we can write with the params on the left as









QUIZ

What is the type of quiz ?

A. Int -> Int

B. Int -> Bool

C. Int -> Int -> Int

D. Int -> Int -> Bool

E. (Int, Int) -> Bool









Function Calls

A function call is exactly like in the λ-calculus

where e1 is a function and e2 is the argument. For example









Multiple Argument Calls

With multiple arguments, just pass them in one by one, e.g.

For example









EXERCISE

Write a function myMax that returns the maximum of two inputs

When you are done you should see the following behavior:









How to Return Multiple Outputs?









Tuples

A type for packing n different kinds of values into a single “struct”

For example









QUIZ

What is the type ??? of tup3?

A. (Int, Bool)

B. (Int, Double, Bool)

C. (Int, (Double, Bool))

D. ((Int, Double), Bool)

E. (Tuple, Bool)









Extracting Values from Tuples

We can create a tuple of three values e1, e2, and e3 …

… but how to extract the values from this tuple?

Pattern Matching









QUIZ

What is the value of quiz defined as

A. 'a'

B. 5.2

C. 7

D. ('a', 5.2)

E. (5.2, 7)









Lists

Unbounded Sequence of values of type T

For example









QUIZ

What is the type of things defined as

A. [Int]

B. ([Int], [Int], [Int])

C. [(Int, Int, Int)]

D. [[Int]]

E. List









List’s Values Must Have The SAME Type!

The type [T] denotes an unbounded sequence of values of type T

Suppose you have a list

There is no T that we can use

  • As last element is not Int
  • First two elements are not Char!

Result: Mysterious Type Error!









Constructing Lists

There are two ways to construct lists

For example

Cons Operator : is Right Associative

x1 : x2 : x3 : x4 : t means x1 : (x2 : (x3 : (x4 : t)))

So we can just avoid the parentheses.

Syntactic Sugar

Haskell lets you write [x1, x2, x3, x4] instead of x1 : x2 : x3 : x4 : []









Functions Producing Lists

Lets write a function copy3 that

  • takes an input x and
  • returns a list with three copies of x

When you are done, you should see the following









PRACTICE: Clone

Write a function clone such that clone n x returns a list with n copies of x.

When you are done you should see the following behavior















How does clone execute?

(Substituting equals-by-equals!)














EXERCISE: Range

Write a function range such that range i j returns the list of values [i, i+1, ..., j]

When we are done you should get the behavior









Functions Consuming Lists

So far: how to produce lists.

Next how to consume lists!
















Example

Lets write a function firstElem such that firstElem xs returns the first element xs if it is a non-empty list, and 0 otherwise.

When you are done you should see the following behavior:









QUIZ

Suppose we have the following mystery function

What does mystery [10, 20, 30] evaluate to?

A. 10

B. 20

C. 30

D. 3

E. 0









EXERCISE: Summing a List

Write a function sumList such that sumList [x1, ..., xn] returns x1 + ... + xn

When you are done you should get the following behavior:

Recap

  • Core program element is an expression
  • Every valid expression has a type (determined at compile-time)
  • Every valid expression reduces to a value (computed at run-time)

Execution

  • Basic values & operators

  • Execution / Function Calls just substitute equals by equals

  • Pack data into tuples & lists

  • Unpack data via pattern-matching