Recap: Haskell Crash Course II

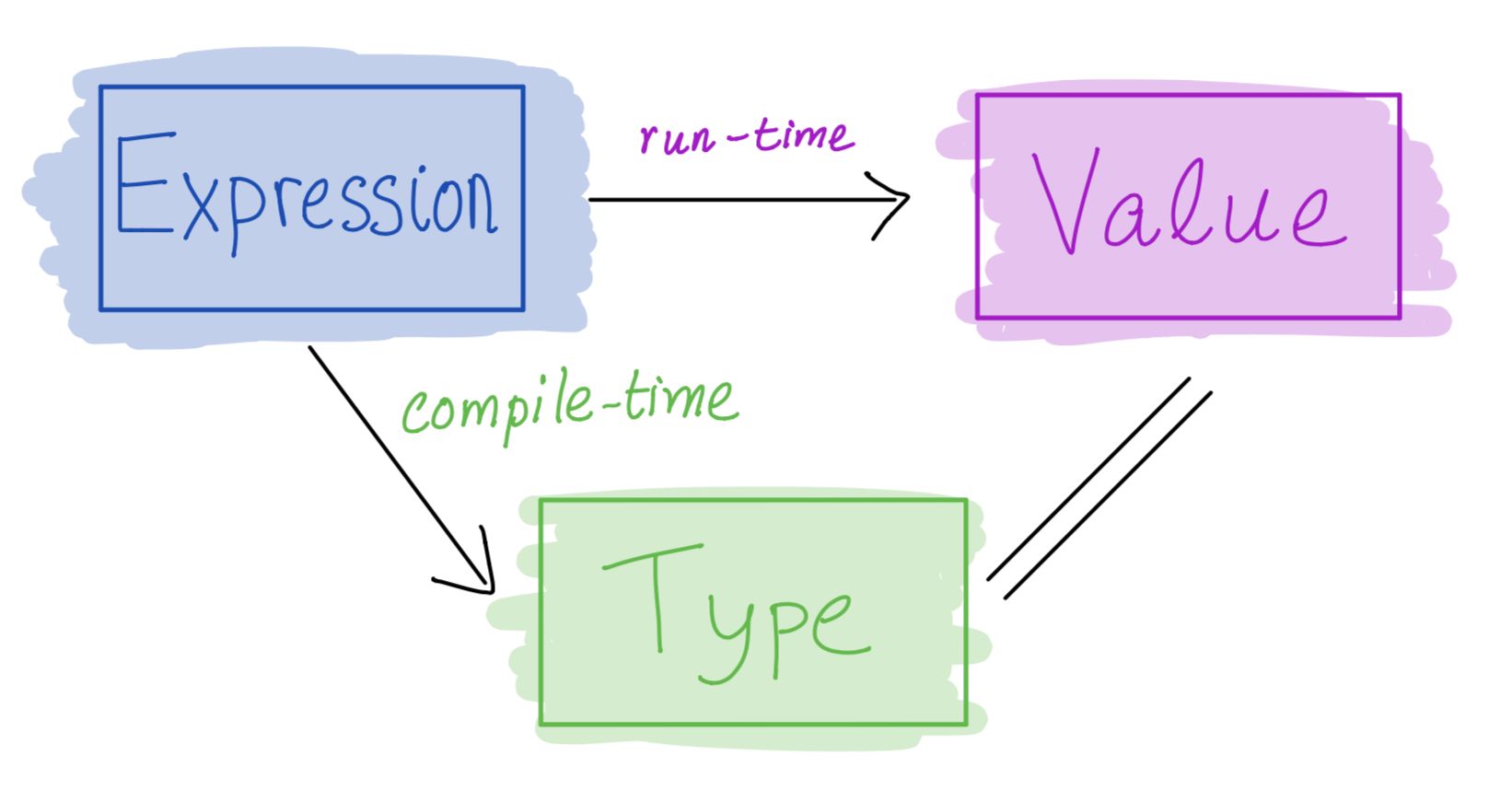
• Core program element is an expression
• Every valid expression has a type (determined at compile-time)
• Every valid expression reduces to a value (computed at run-time)

Recap: Haskell

Basic values & operators

• Int, Bool, Char, Double
• +, -, ==, /=

Execution / Function Calls

• Just substitute equals by equals

Producing Collections

• Pack data into tuples & lists

Consuming Collections

• Unpack data via pattern-matching

Next: Creating and Using New Data Types

1. type Synonyms: Naming existing types

2. data types: Creating new types

Type Synonyms

Synonyms are just names (“aliases”) for existing types

• think typedef in C

A type to represent Circle

A tuple (x, y, r) is a circle with center at (x, y) and radius r

type Circle = (Double, Double, Double)

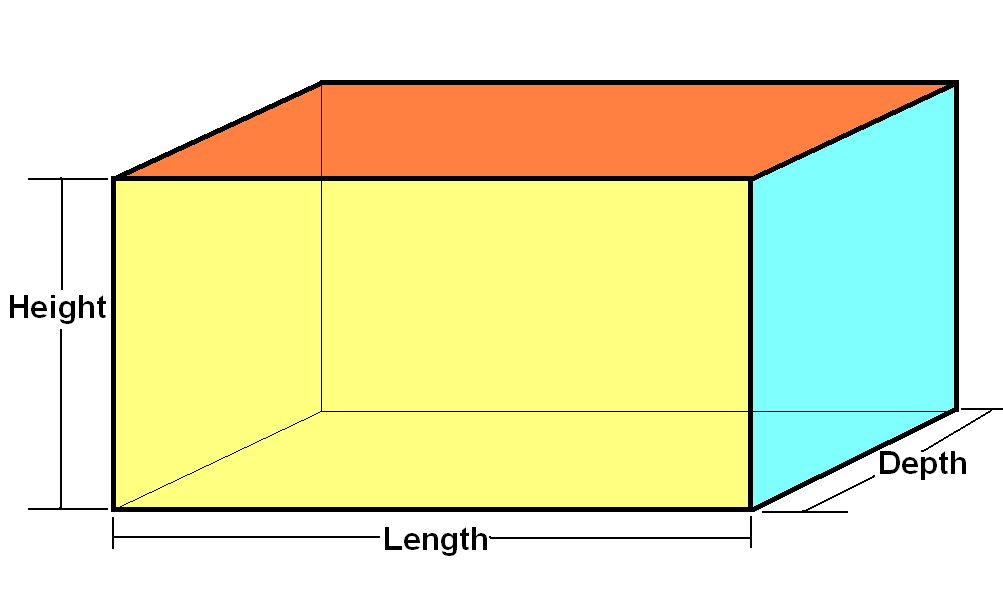
A type to represent Cuboid

A tuple (length, depth, height) is a cuboid

type Cuboid = (Double, Double, Double)

Using Type Synonyms

We can now use synonyms by creating values of the given types

circ0 :: Circle 
circ0 = (0, 0, 100)  -- ^ circle at "origin" with radius 100

cub0 :: Cuboid
cub0 = (10, 20, 30)  -- ^ cuboid with length=10, depth=20, height=30 

And we can write functions over synonyms too

area :: Circle -> Double
area (x, y, r) = pi * r * r  

volume :: Cuboid -> Double
volume (l, d, h) = l * d * h 

We should get this behavior

>>> area circ0 
31415.926535897932

>>> volume cub0
6000

QUIZ

Suppose we have the definitions

type Circle = (Double, Double, Double)
type Cuboid = (Double, Double, Double)

circ0 :: Circle 
circ0 = (0, 0, 100)  -- ^ circle at "origin" with radius 100

cub0 :: Cuboid
cub0 = (10, 20, 30)  -- ^ cuboid with length=10, depth=20, height=30 

area :: Circle -> Double
area (x, y, r) = pi * r * r  

volume :: Cuboid -> Double
volume (l, d, h) = l * d * h

What is the result of

>>> volume circ0

A. 0

B. Type error

Beware!

Type Synonyms

• Do not create new types

• Just name existing types

And hence, synonyms

• Do not prevent confusing different values

Creating New Data Types

We can avoid mixing up by creating new data types

-- | A new type `CircleT` with constructor `MkCircle`
data CircleT = MkCircle Double Double Double     

-- | A new type `CuboidT` with constructor `MkCuboid`
data CuboidT = MkCuboid Double Double Double

Constructors are the only way to create values

• MkCircle creates CircleT

• MkCuboid creates CuboidT

QUIZ

Suppose we create a new type with a data definition

-- | A new type `CircleT` with constructor `MkCircle`
data CircleT = MkCircle Double Double Double     

What is the type of the MkCircle constructor?

A. MkCircle :: CircleT

B. MkCircle :: Double -> CircleT

C. MkCircle :: Double -> Double -> CircleT

D. MkCircle :: Double -> Double -> Double -> CircleT

E. MkCircle :: (Double, Double, Double) -> CircleT

Constructing Data

Constructors let us build values of the new type

circ1 :: CircleT 
circ1 = MkCircle 0 0 100  -- ^ circle at "origin" w/ radius 100

cub1 :: Cuboid
cub1 = MkCuboid 10 20 30  -- ^ cuboid w/ len=10, dep=20, ht=30 

QUIZ

Suppose we have the definitions

data CuboidT = MkCuboid Double Double Double     

type Cuboid  = (Double, Double, Double)

volume :: Cuboid -> Double
volume (l, d, h) = l * d * h

What is the result of

>>> volume (MkCuboid 10 20 30)

A. 6000

B. Type error

Deconstructing Data

Constructors let us build values of new type … but how to use those values?

How can we implement a function

volume :: Cuboid -> Double
volume c = ???

such that

>>> volume (MkCuboid 10 20 30)
6000

Deconstructing Data by Pattern Matching

Haskell lets us deconstruct data via pattern-matching

volume :: Cuboid -> Double
volume c = case c of
             MkCuboid l d h -> l * d * h

case e of Ctor x y z -> e1 is read as as

IF - e evaluates to a value that matches the pattern Ctor vx vy vz

THEN - evaluate e1 after naming x := vx, y := vy, z := vz

Pattern matching on Function Inputs

Very common to do matching on function inputs

volume :: Cuboid -> Double
volume c = case c of 
            MkCuboid l d h -> l * d * h

area :: Circle -> Double
area a  = case a of 
            MkCircle x y r -> pi * r * r

So Haskell allows a nicer syntax: patterns in the arguments

volume :: Cuboid -> Double
volume (MkCuboid l d h) = l * d * h

area :: Circle -> Double
area (MkCircle x y r) = pi * r * r

Nice syntax plus the compiler saves us from mixing up values!

But … what if we need to mix up values?

Suppose I need to represent a list of shapes

• Some Circles
• Some Cuboids

What is the problem with shapes as defined below?

shapes = [circ1, cub1]

Where we have defined

circ1 :: CircleT 
circ1 = MkCircle 0 0 100  -- ^ circle at "origin" with radius 100

cub1 :: Cuboid
cub1 = MkCuboid 10 20 30  -- ^ cuboid with length=10, depth=20, height=30 

Problem: All list elements must have the same type

Solution???

QUIZ: Variant (aka Union) Types

Lets create a single type that can represent both kinds of shapes!

data Shape 
  = MkCircle Double Double Double   -- ^ Circle at x, y with radius r 
  | MkCuboid Double Double Double   -- ^ Cuboid with length, depth, height

What is the type of MkCircle 0 0 100 ?

A. Shape

B. Circle

C. (Double, Double, Double)

Each Data Constructor of Shape has a different type

When we define a data type like the below

data Shape 
  = MkCircle  Double Double Double   -- ^ Circle at x, y with radius r 
  | MkCuboid  Double Double Double   -- ^ Cuboid with length, depth, height

We get multiple constructors for Shape

MkCircle :: Double -> Double -> Double -> Shape
MkCuboid :: Double -> Double -> Double -> Shape

Now we can create collections of Shape

Now we can define

circ2 :: Shape
circ2 = MkCircle 0 0 100  -- ^ circle at "origin" with radius 100

cub2 :: Shape 
cub2 = MkCuboid 10 20 30  -- ^ cuboid with length=10, depth=20, height=30 

and then define collections of Shapes

shapes :: [Shape]
shapes = [circ1, cub1]

EXERCISE

Lets define a type for 2D shapes

data Shape2D 
  = MkRect Double Double -- ^ 'MkRect w h' is a rectangle with width 'w', height 'h'
  | MkCirc Double        -- ^ 'MkCirc r' is a circle with radius 'r'
  | MkPoly [Vertex]      -- ^ 'MkPoly [v1,...,vn]' is a polygon with vertices at 'v1...vn'

type Vertex = (Double, Double)

Write a function to compute the area of a Shape2D

area2D :: Shape2D -> Double
area2D s = ???

HINT

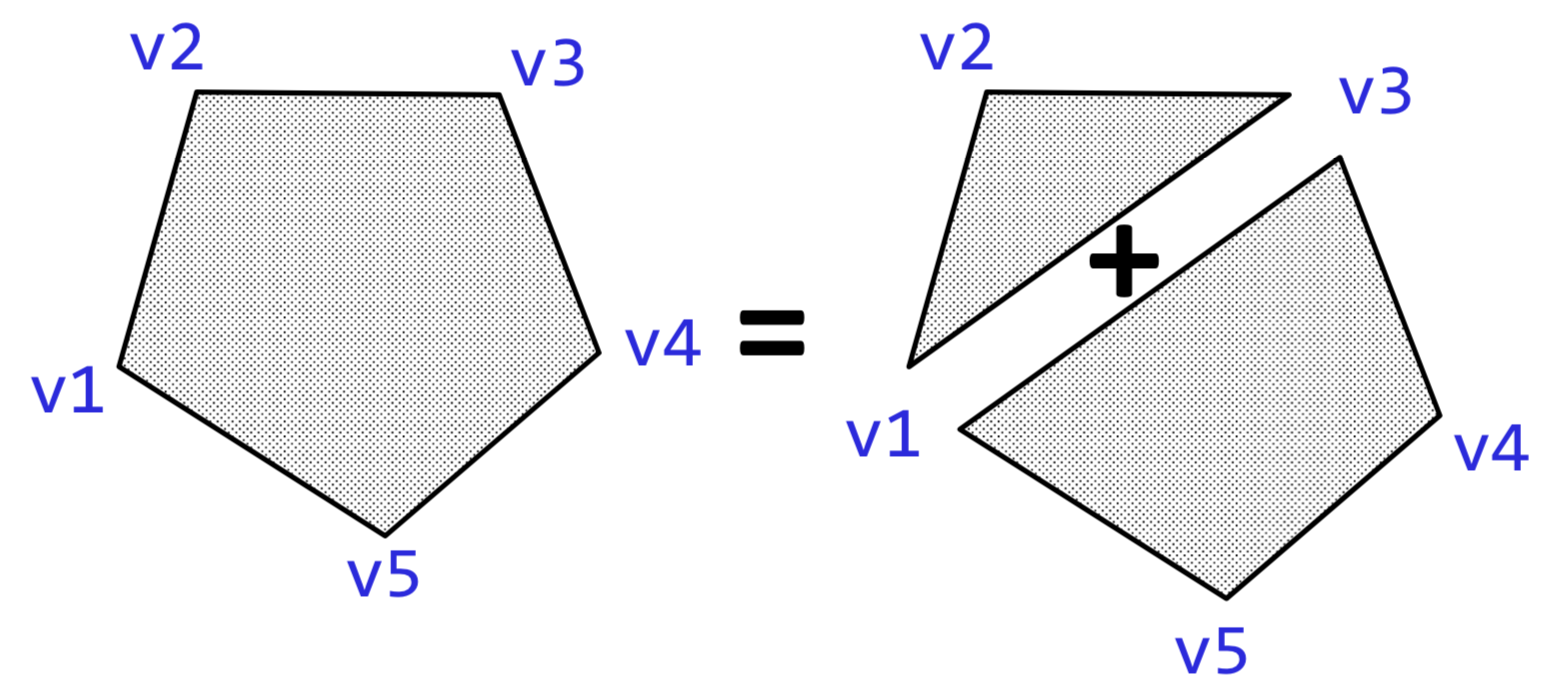
You may want to use this helper that computes the area of a triangle at v1, v2, v3

areaTriangle :: Vertex -> Vertex -> Vertex -> Double
areaTriangle v1 v2 v3 = sqrt (s * (s - s1) * (s - s2) * (s - s3))
  where 
      s  = (s1 + s2 + s3) / 2
      s1 = distance v1 v2 
      s2 = distance v2 v3
      s3 = distance v3 v1

distance :: Vertex -> Vertex -> Double
distance (x1, y1) (x2, y2) = sqrt ((x2 - x1) ** 2 + (y2 - y1) ** 2)