Before we continue …

A Word from the Sponsor!

		Don't Fear Monads

They are just a versatile abstraction, like map or fold.

Parsers

A parser is a function that

• converts unstructured data (e.g. String, array of Byte,…)
• into structured data (e.g. JSON object, Markdown, Video…)

type Parser = String -> StructuredObject

Every large software system contains a Parser

How to build Parsers?

Two standard methods

Regular Expressions

• Doesn’t really scale beyond simple things
• No nesting, recursion

Parser Generators

1. Specify grammar via rules

Expr : Var            { EVar $1       }
     | Num            { ENum $1       }
     | Expr Op Expr   { EBin $1 $2 $3 }
     | '(' Expr ')'   { $2            }
     ;

2. Tools like yacc, bison, antlr, happy

• convert grammar into executable function

Grammars Don’t Compose!

If we have two kinds of structured objects Thingy and Whatsit.

Thingy : rule 	{ action } 
;

Whatsit : rule  { action }
;

To parse sequences of Thingy and Whatsit we must duplicate the rules

Thingies : Thingy Thingies  { ... } 
           EmptyThingy      { ... }
;

Whatsits : Whatsit Whatsits { ... }
           EmptyWhatsit     { ... }
;

No nice way to reuse the sub-parsers for Whatsit and Thingy :-(

A New Hope: Parsers as Functions

Lets think of parsers directly as functions that

• Take as input a String
• Convert a part of the input into a StructuredObject
• Return the remainder unconsumed to be parsed later

data Parser a = P (String -> (a, String))

A Parser a

• Converts a prefix of a String
• Into a structured object of type a and
• Returns the suffix String unchanged

Parsers Can Produce Many Results

Sometimes we want to parse a String like

"2 - 3 - 4"

into a list of possible results

[(Minus (Minus 2 3) 4),   Minus 2 (Minus 3 4)]

So we generalize the Parser type to

data Parser a = P (String -> [(a, String)])

EXERCISE

Given the definition

data Parser a = P (String -> [(a, String)])

Implement a function

runParser :: Parser a -> String -> [(a, String)]
runParser p s = ???

QUIZ

Given the definition

data Parser a = P (String -> [(a, String)])

Which of the following is a valid Parser Char

• that returns the first Char from a string (if one exists)

-- A
oneChar = P (\cs -> head cs)

-- B
oneChar = P (\cs -> case cs of 
                      []   -> [('', []) 
                      c:cs -> (c, cs))

-- C
oneChar = P (\cs -> (head cs, tail cs))

-- D
oneChar = P (\cs -> [(head cs, tail cs)])

-- E
oneChar = P (\cs -> case cs of
                      [] -> [] 
                      cs -> [(head cs, tail cs)])

Lets Run Our First Parser!

>>> runParser oneChar "hey!"
[('h', "ey")]

>>> runParser oneChar "yippee"
[('y', "ippee")]

>>> runParser oneChar ""
[]

Failure to parse means result is an empty list!

EXERCISE

Your turn: Write a parser to grab first two chars

twoChar :: Parser (Char, Char)
twoChar = P (\cs -> ???) 

When you are done, we should get

>>> runParser twoChar "hey!"
[(('h', 'e'), "y!")]

>>> runParser twoChar "h"
[]

QUIZ

Ok, so recall

twoChar :: Parser (Char, Char)
twoChar  = P (\cs -> case cs of
                       c1:c2:cs' -> [((c1, c2), cs')]
                       _         -> [])

Suppose we had some foo such that twoChar' was equivalent to twoChar

twoChar' :: Parser (Char, Char)
twoChar' = foo oneChar oneChar 

What must the type of foo be?

A. Parser (Char, Char)

B. Parser Char -> Parser (Char, Char)

C. Parser a -> Parser a -> Parser (a, a)

D. Parser a -> Parser b -> Parser (a, b)

E. Parser a -> Parser (a, a)

EXERCISE: A forEach Loop

Lets write a function

forEach :: [a] -> (a -> [b]) -> [b]
forEach xs f = ???

such that we get the following behavior

>>> forEach [] (\i -> [i, i + 1])
[]

>>> forEach [10,20,30] (\i -> [show i, show (i+1)])
["10", "11", "20", "21", "30", "31"]

QUIZ

What does quiz evaluate to?

quiz = forEach [10, 20, 30] (\i -> 
         forEach [0, 1, 2] (\j -> 
           [i + j] 
         )
       )

A. [10,20,30,0,1,2]

B. [10,0,20,1,30,2]

C. [[10,11,12], [20,21,22] [30,31,32]]

D. [10,11,12,20,21,22,30,31,32]

E. [32]

A pairP Combinator

Lets implement the above as pairP

forEach :: [a] -> (a -> [b]) -> [b]
forEach xs f = concatMap f xs 

pairP :: Parser a -> Parser b -> Parser (a, b)
pairP aP bP = P (\s -> forEach (runParser aP s) (\(a, s') ->
                         forEach (runParser bP s') (\(b, s'') -> 
                           ((a, b), s'')
                       )
                ) 

Now we can write

twoChar = pairP oneChar oneChar

QUIZ

What does quiz evaluate to?

twoChar = pairP oneChar oneChar

quiz    = runParser twoChar "h" 

A. [((h,h), "")]

B. [(h, "")]

C. [("", "")]

D. []

E. Run-time exception

Does the Parser a type remind you of something?

Lets implement the above as pairP

data Parser a = P (String -> [(a, String)])

data ST s a   = S (s -> (a, s))

Parser is a Monad!

Like a state transformer, Parser is a monad!

We need to implement two functions

returnP :: a -> Parser a

bindP   :: Parser a -> (a -> Parser b) -> Parser b

QUIZ

Which of the following is a valid implementation of returnP

data Parser a = P (String -> [(a, String)])

returnP   :: a -> Parser a

returnP a = P (\s -> [])          -- A

returnP a = P (\s -> [(a, s)])    -- B

returnP a = P (\s -> (a, s))      -- C

returnP a = P (\s -> [(a, "")])   -- D

returnP a = P (\s -> [(s, a)])    -- E

HINT: return a should just

• “produce” the parse result a and
• leave the string unconsumed.

Bind

Next, lets implement bindP

• we almost saw it as pairP

bindP :: Parser a -> (a -> Parser b) -> Parser b
bindP aP fbP = P (\s -> 
  forEach (runParser aP s) (\(a, s') -> 
    forEach (runParser (fbP a) s') (\(b, s'') ->
      [(b, s'')]
    )   
  )
)

The function

• Builds the a values out of aP (using runParser)
• Builds the b values by calling fbP a on the remainder string s'
• Returns b values and the remainder string s''

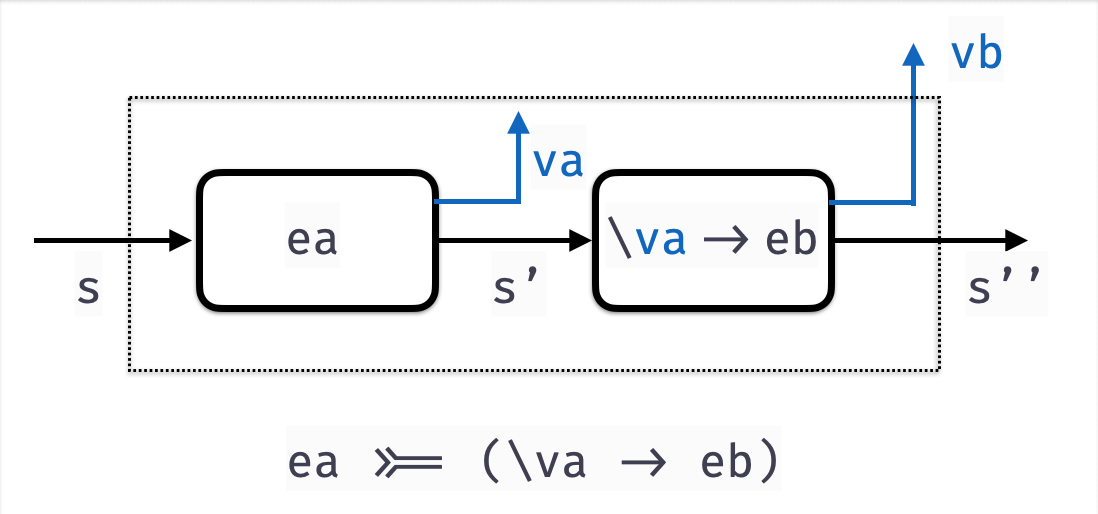
The Parser Monad

We can now make Parser an instance of Monad

instance Monad Parser where
  (>>=)  = bindP
  return = returnP

And now, let the wild rumpus start!

Parser Combinators

Lets write lots of high-level operators to combine parsers!

Here’s a cleaned up pairP

pairP :: Parser a -> Parser b -> Parser (a, b)
pairP aP bP = do 
  a <- aP
  b <- bP
  return (a, b)

Failures are the Pillars of Success!

Surprisingly useful, always fails

• i.e. returns [] no successful parses

failP :: Parser a
failP = P (\_ -> [])

QUIZ

Consider the parser

satP :: (Char -> Bool) -> Parser Char
satP p = do 
  c <- oneChar
  if p c then return c else failP

What is the value of

quiz1 = runParser (satP (\c -> c == 'h')) "hellow"
quiz2 = runParser (satP (\c -> c == 'h')) "yellow"

Parsing Alphabets and Numerics

We can now use satP to write

-- parse ONLY the Char c
char :: Parser Char
char c = satP (\c' -> c == c')

-- parse ANY ALPHABET 
alphaCharP :: Parser Char
alphaCharP = satP isAlpha

-- parse ANY NUMERIC DIGIT
digitChar :: Parser Char
digitChar = satP isDigit

QUIZ

We can parse a single Int digit

digitInt :: Parser Int
digitInt = do
  c <- digitChar      -- parse the Char c
  return (read [c])   -- convert Char to Int

What is the result of

quiz1 = runParser digitInt "92"
quiz2 = runParser digitInt "cat"

EXERCISE

Write a function

strP :: String -> Parser String 
strP s = -- parses EXACTLY the String s and nothing else

when you are done, we should get the following behavior

>>> dogeP = strP "doge"

>>> runParser dogeP "dogerel"
[("doge", "rel")]

>>> runParser dogeP "doggoneit"
[]

A Choice Combinator

Lets write a combinator orElse p1 p2 such that

• returns the results of p1

or, else if those are empty

• returns the results of p2

:: Parser a -> Parser a -> Parser a
orElse p1 p2 = -- produce results of `p1` if non-empty
               -- OR-ELSE results of `p2`

e.g. orElseP lets us build a parser that produces an alphabet OR a numeric character

alphaNumChar :: Parser Char
alphaNumChar = alphaChar `orElse` digitChar

Which should produce

>>> runParser alphaNumChar "cat"
[('c', "at")]

>>> runParser alphaNumChar "2cat"
[('2', "cat")]

>>> runParser alphaNumChar "230"
[('2', "30")]

QUIZ

orElse :: Parser a -> Parser a -> Parser a
orElse p1 p2 = -- produce results of `p1` if non-empty
               -- OR-ELSE results of `p2`

Which of the following implements orElse?

-- a 
orElse p1 p2 = do 
  r1s <- p1
  r2s <- p2
  return (r1s ++ r2s) 

-- b
orElse p1 p2 = do 
  r1s <- p1 
  case r1s of 
    [] -> p2 
    _  -> return r1s

-- c
orElse p1 p2 = P (\cs -> 
  runParser p1 cs ++ runParser p2 cs
  )

-- d
orElse p1 p2 = P (\cs -> 
  case runParser p1 cs of
    []  -> runParser p2 cs
    r1s -> r1s
  )

An “Operator” for orElse

It will be convenient to have a short “operator” for orElse

p1 <|> p2 = orElse p1 p2

A Simple Expression Parser

Now, lets write a tiny calculator!

-- 1. First, parse the operator 
intOp      :: Parser (Int -> Int -> Int) 
intOp      = plus <|> minus <|> times <|> divide 
  where 
    plus   = do { _ <- char '+'; return (+) }
    minus  = do { _ <- char '-'; return (-) }
    times  = do { _ <- char '*'; return (*) }
    divide = do { _ <- char '/'; return div }

-- 2. Now parse the expression!
calc :: Parser Int
calc = do x  <- digitInt
          op <- intOp
          y  <- digitInt 
          return (x `op` y)

When calc is run, it will both parse and calculate

>>> runParser calc "8/2"
[(4,"")]

>>> runParser calc "8+2cat"
[(10,"cat")]

>>> runParser calc "8/2cat"
[(4,"cat")]

>>> runParser calc "8-2cat"
[(6,"cat")]

>>> runParser calc "8*2cat"
[(16,"cat")]

QUIZ

What will quiz evaluate to?

calc :: Parser Int
calc = do x  <- digitInt
          op <- intOp
          y  <- digitInt 
          return (x `op` y)

quiz = runParser calc "99bottles"

A. Type error

B. []

C. [(9, "9bottles")]

D. [(99, "bottles")]

E. Run-time exception

Next: Recursive Parsing

Its cool to parse individual Char …

… but way more interesting to parse recursive structures!

"((2 + 10) * (7 - 4)) * (5 + 2)"

EXERCISE: A “Recursive” String Parser

The parser string s parses exactly the string s - fails otherwise

>>> runParser (string "mic") "mickeyMouse"
[("mic","keyMouse")]

>>> runParser (string "mic") "donald duck"
[]

Lets fill in an implementation

string :: String -> Parser String
string s = ???

Which library function will eliminate the recursion from string?

QUIZ: Parsing Many Times

Often we want to repeat parsing some object

-- | `manyP p` repeatedly runs `p` to return a list of [a]
manyP  :: Parser a -> Parser [a]
manyP p = m0 <|> m1
  where
    m0  = return [] 
    m1  = do { x <- p; xs <- manyP p; return (x:xs) } 

Recall digitChar :: Parser Char returned a single numeric Char

What will quiz evaluate to?

quiz = runParser (manyP digitChar) "123horse"

A. [("" , "1234horse")]

B. [("1" , "234horse")]

C. [("1", "23horse"), ("12", "3horse"), ("123", "horse )]

D. [("123", "horse")]

E. []

Lets fix manyP!

Run p first and only return [] if it fails …

-- | `manyP p` repeatedly runs `p` to return a list of [a]
manyP  :: Parser a -> Parser [a]
manyP p = m1 <|> m0
  where
    m0  = return [] 
    m1  = do { x <- p; xs <- manyP p; return (x:xs) } 

now, we can write an Int parser as

int :: Parser Int
int = do { xs <- manyP digitChar; return (read xs) }

which will produce

>>> runParser oneChar "123horse"
[("123", "horse")]

>>> runParser int "123horse"
[(123, "horse")]

Parsing Arithmetic Expressions

Now we can build a proper calculator!

calc0 ::  Parser Int
calc0 = binExp <|> int 

int :: Parser Int
int = do 
  xs <- many digitChar 
  return (read xs)

binExp :: Parser Int
binExp = do
  x <- int 
  o <- intOp 
  y <- calc0 
  return (x `o` y) 

Works pretty well!

>>> runParser calc0 "11+22+33"
[(66,"")]

ghci> doParse calc0 "11+22-33"
[(0,"")]

QUIZ

calc0 ::  Parser Int
calc0 = binExp <|> int 

int :: Parser Int
int = do 
  xs <- many digitChar 
  return (read xs)

binExp :: Parser Int
binExp = do
  x <- int 
  o <- intOp 
  y <- calc0 
  return (x `o` y) 

What does quiz evaluate to?

quiz = runParser calc0 "10-5-5"

A. [(0, "")]

B. []

C. [(10, "")]

D. [(10, "-5-5")]

E. [(5, "-5")]

Problem: Right-Associativity

Recall

binExp :: Parser Int
binExp = do
  x <- int 
  o <- intOp 
  y <- calc0 
  return (x `o` y)

"10-5-5" gets parsed as 10 - (5 - 5) because

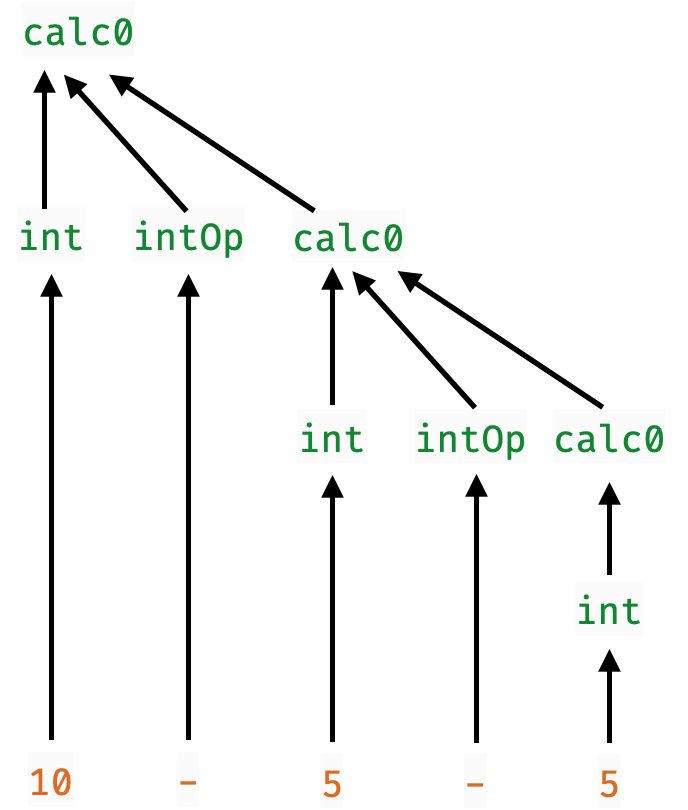
The calc0 parser implicitly forces each operator to be right associative

• doesn’t matter for +, *

• but is incorrect for -

QUIZ

Recall

binExp :: Parser Int
binExp = do
  x <- int 
  o <- intOp 
  y <- calc0 
  return (x `o` y)

What does quiz get evaluated to?

quiz = runParser calc0 "10*2+100"

A. [(1020,"")]

B. [(120,"")]

C. [(120,""), (1020, "")]

D. [(1020,""), (120, "")]

E. []

The calc0 parser implicitly forces all operators to be right associative

• doesn’t matter for +, *

• but is incorrect for -

Does not respect precedence!

Simple Fix: Parentheses!

Lets write a combinator that parses something within (...)

parensP :: Parser a -> Parser a
parensP p = do 
  _ <- char '(' 
  x <- p
  _ <- char ')'
  return x 

now we can try

calc1 :: Parser Int
calc1 = parens binExp <|> int 

binExp :: Parser Int
binExp = do
  x <- int 
  o <- intOp 
  y <- calc1 
  return (x `o` y)

now the original string wont even parse

>>> runParser calc1 "10-5-5" 
[]

but we can add parentheses to get the right result

>>> runParser calc1 "((10-5)-5)" 
[(0 ,"")]

>>> runParser calc1 "(10-(5-5))" 
[(10 ,"")]

>>> runParser calc1 "((10*2)+100)"
[(120, "")]

>>> runParser calc1 "(10*(2+100))"
[(1020, "")]

Left Associativity

But how to make the parser left associative

• i.e. parse “10-5-5” as (10 - 5) - 5 ?

Lets flip the order!

calc1      ::  Parser Int
calc1      = binExp <|> oneInt 

binExp :: Parser Int
binExp = do 
  x <- calc1 
  o <- intOp 
  y <- int
  return (x `o` y)

But …

>>> runParser calc1 "2+2"
...

Infinite loop! calc1 --> binExp --> calc1 --> binExp --> ...

• without consuming any input :-(

Solution: Parsing with Multiple Levels

Any expression is a sum-of-products

  10 * 20 * 30 + 40 * 50 + 60 * 70 * 80
=> 
  ((((10 * 20) * 30) + (40 * 50)) + ((60 * 70) * 80))
=>  
  ((((base * base) * base)  + (base * base)) + ((base * base) * base))
=>  
  (((prod * base) + prod)  + (prod * base))
=>  
  ((prod + prod) + prod) 
=>   
  (sum + prod)
=>
   sum 
=>   
   expr

Parsing with Multiple Levels

So lets layer our language as

  expr :== sum
  sum  :== (((prod "+" prod) "+" prod) "+" ... "+" prod)
  prod :== (((base "*" base) "*" base) "*" ... "*" base) 
  base :== "(" expr ")" ORELSE int

that is the recursion looks like

  expr = sum
  sum  = oneOrMore prod "+" 
  prod = oneOrMore base "*"
  base = "(" expr ")" <|> int 

No infinite loop!

• expr --> prod --> base -->* expr

• but last step -->* consumes a (

Parsing oneOrMore

Lets implement oneOrMore vP oP as a combinator - vP parses a single a value - oP parses an operator a -> a -> a - oneOrMore vP oP parses and returns the result ((v1 o v2) o v3) o v4) o ... o vn)

But how?

1. grab the first v1 using vP

2. continue by
   • either trying oP then v2 … and recursively continue with v1 o v2
   • orElse (no more o) just return v1

oneOrMore :: Parser a -> Parser (a -> a -> a) -> Parser a
oneOrMore vP oP = do {v1 <- vP; continue v1}
  where 
    continue v1 = do { o <- oP; v2 <- vP; continue (v1 `o` v2) }
               <|> return v1

Implementing Layered Parser

Now we can implement the grammar

  expr = sum
  sum  = oneOrMore prod "+" 
  prod = oneOrMore base "*"
  base = "(" expr ")" <|> int 

simply as

expr = sum
sum  = oneOrMore prod addOp
prod = oneOrMore base mulOp
base = parens expr <|> int

where addOp is + or - and mulOp is * or /

addOp, mulOp :: Parser (Int -> Int -> Int)
addOp = constP "+" (+) <|> constP "-" (-)
mulOp = constP "*" (*) <|> constP "/" div

constP :: String -> a -> Parser a 
constP s x = do { _ <- string s; return x }

Lets make sure it works!

>>> doParse sumE2 "10-1-1"
[(8,"")]

>>> doParse sumE2 "10*2+1"
[(21,"")]

>>> doParse sumE2 "10+2*1"
[(12,"")]

Parser combinators

That was a taste of Parser Combinators

• Transferred from Haskell to many other languages.

Many libraries including Parsec used in your homework - oneOrMore is called chainl

Read more about the theory - in these recent papers

Read more about the practice - in this recent post that I like JSON parsing from scratch