Monads Can Be Used for Many Things!

• Partial Functions
• Global Variables
• Parsing
• Exceptions
• Test Generation
• Concurrency
• …

Exception Handling

Recall our expressions with division

data Expr
  = Number Int            -- ^ 0,1,2,3,4
  | Plus   Expr Expr      -- ^ e1 + e2
  | Div    Expr Expr      -- ^ e1 / e2
  deriving (Show)

We had a potentially crashing evaluator

eval :: Expr -> Int
eval (Number n)    = n
eval (Plus  e1 e2) = eval e1   +   eval e2
eval (Div   e1 e2) = eval e1 `div` eval e2

-- >>> eval (Div (Val 10) (Plus (Number 5) (Number (-5))))
-- Exception: Divide by zero

We defined a Result type

data Result a = Ok a | Err String

made it a Monad

instance Monad Result where
  return x      = Ok x
  (Ok v)  >>= f = f v
  (Err s) >>= _ = Err s

and then we can write

eval :: Expr -> Result Int
eval (Number n)    = return n
eval (Plus  e1 e2) = do {n1 <- eval e1; n2 <- eval e2; return (n1   +   n2) } 
eval (Div   e1 e2) = do { n1 <- eval e1; 
                          n2 <- eval e2; 
                          if n2 /= 0 
                            then return (n1 `div` n2) 
                            else Err ("DBZ: " ++ show e2)
                        }

which doesn’t crash but returns an Err

>>> eval (Div (Number 10) (Plus (Number 5) (Number (-5))))
Err "DBZ: Plus (Number 5) (Number (-5))"

and when it succeeds it returns an Ok

>>> eval (Div (Number 10) (Plus (Number 5) (Number (-5))))
Ok 1

Generalizing Result to Either

The standard library generalizes the Result type to Either

data Result   a = Err String | Ok a 

data Either e a = Left e     | Right a

• Err s becomes Left s
• Ok v becomes Right v
• Result a becomes Either String a

(But we can data other than String in the Left values)

EXERCISE: Generalizing Result Monad to Either Monad

Lets translate the old Monad instance for Result

instance Monad Result where

  -- return :: a -> Result a
  return x      = Ok x

  -- (>>=) :: Result a -> (a -> Result b) -> Result b
  (Ok v)  >>= f = f v
  (Err s) >>= _ = s

into a Monad instance for Either

instance Monad (Either e) where
  -- return :: a -> Either e a
  return x        = ???

  -- (>>=) :: Either e a -> (a -> Either e b) -> Either e b
  (Right v) >>= f = ???  
  (Left  s) >>= _ = ??? 

QUIZ

We can rewrite eval to return an Either

eval :: Expr -> Either Expr Int
eval (Number n)    = return n
eval (Plus  e1 e2) = do n1 <- eval e1 
                        n2 <- eval e2
                        return (n1+n2)
eval (Div   e1 e2) = do n1 <- eval e1 
                        n2 <- eval e2
                        if n2 /= 0 
                          then return (n1 `div` n2) 
                          else Left e2

What does quiz evaluate to?

quiz = eval (Div (Val 10) (Plus (Number 5) (Number (-5))))

A. Err "DBZ: Plus (Number 5) (Number (-5))"

B. Left "DBZ: Plus (Number 5) (Number (-5))"

C. Run-time Exception

D. Plus (Number 5) (Number (-5))

E. Left (Plus (Number 5) (Number (-5)))

Either is an Exception Monad!

What can you do with exceptions?

1. throwError an exception (with some value) …

2. catchError an exception (and use its value) …

1. throwing an Exception

We can simply define

throw :: e -> Either e a
throw exn = Left exn

and now voila

eval :: Expr -> Either Expr Int
eval (Number n)    = return n
eval (Plus  e1 e2) = do n1 <- eval e1 
                        n2 <- eval e2
                        return (n1 + n2)
eval (Div   e1 e2) = do n1 <- eval e1 
                        n2 <- eval e2
                        if n2 /= 0 
                          then return (n1 `div` n2) 
                          else throw e2

Exactly the same evaluator

• Result is a Left ==> an exception came all the way to the top.

• Either monad ensures the “exception” shoots to the top!

>>> eval (Div (Numer 10) (Plus (Number 5) (Number (-5))))
Left (Minus (Number 5) (Number 5))

No further evaluation happens after a throw because ???

catching an exception

How to catch an exception?

Lets change our Expr type to

data Expr
  = Number  Int            -- ^ 0,1,2,3,4
  | Plus    Expr Expr      -- ^ e1 + e2
  | Try     Expr Int       
  deriving (Show)

Informally, try e n evaluates to e but

• if e is undefined due to divide-by-zero

• then evaluate to n

eval :: Expr -> Either Expr Int
eval (Number n)    = return n
eval (Plus  e1 e2) = do n1 <- eval e1 
                        n2 <- eval e2
                        return (n1+n2)
eval (Div   e1 e2) = do n1 <- eval e1 
                        n2 <- eval e2
                        if n2 /= 0 
                          then return (n1 `div` n2) 
                          else throw e2
eval (Try e n)     = catch (eval e) (\_ -> return n)

QUIZ

What should the type of catch be?

A. Either e a -> (a -> Either e b) -> Either e b

B. Either e a -> (e -> Either e b) -> Either e b

C. Either e a -> (e -> Either e a) -> Either e a

D. Either e a -> Either e a -> Either e a

E. Either e a -> Either e b -> Either e b

Implementing catch

Lets implement the catch function!

catch :: Either e a -> (e -> Either e a) -> Either e a
catch (Left  e) handler = ???
catch (Right a) handler = ???

QUIZ

catch :: Either e a -> (e -> Either e a) -> Either e a
catch (Left  e) handle  = ???
catch (Right a) handler = ???

eval :: Expr -> Either Expr Int
eval (Number n)    = return n
eval (Plus  e1 e2) = do n1 <- eval e1 
                        n2 <- eval e2
                        return (n1+n2)
eval (Div   e1 e2) = do n1 <- eval e1 
                        n2 <- eval e2
                        if n2 /= 0 
                          then return (n1 `div` n2) 
                          else throw e2
eval (Try e n)     = catch (eval e) (\_ -> return n)

e1  = Div (Number 10) (Plus (Number 5) (Number (-5)))
e1' = Try e1 7

quiz = eval (Try e1 7)

What does quiz evaluate to?

A. Right 7

B. Left 7

C. Right 0

D. Left 0

E. Left (Plus (Number 5) (Number (-5)))

Either is an Exception Monad!

1. throw an exception (with some value) …

2. catch an exception (and use its value) …

throw :: e -> Either e a
throw e = Left e

catch :: Either e a -> (e -> Either e a) -> Either e a
catch (Left  e) handle = handle e
catch (Right e) _      = Right  e

Monads Can Be Used for Many Things!

• Partial Functions
• Global State
• Parsing
• Exceptions
• Test Generation
• Concurrency
• …

… but what if I want Exceptions and Global State ?

Mixing Monads

What if I want Exceptions and Global State ?

Profiling with the ST Monad

Lets implement a profiling monad that counts the number of operations

-- A State-Transformer with a "global" `Int` counter 
type Profile a = State Int a

We can write a runProfile that

• executes the transformer from 0
• and renders the result

runProfile :: (Show a) => Profile a -> String 
runProfile st = showValCount (runState st 0)

showValCount :: (Show v, Show c) => (v, c) -> String
showValCount (val, count) = "value: " ++ show val ++ ", count: " ++ show count

A function to increment the counter

count :: Profile ()
count = do
  n <- get
  put (n+1)

A Profiling Evaluator

We can use count to write a profiling evaluator

evalProf :: Expr -> Profile Int 
evalProf = eval 
  where
    eval (Number n)    = return n
    eval (Plus  e1 e2) = do n1 <- eval e1 
                            n2 <- eval e2
                            count
                            return (n1+n2)
    eval (Div   e1 e2) = do n1 <- eval e1 
                            n2 <- eval e2
                            count
                            return (n1 `div` n2) 

And now, as there are two operations, we get

>>> e1
Div (Number 10) (Plus (Number 5) (Number 5))

>>> runProfile (evalProf e1)
"value: 1, count: 2"

But what about Divide-by-Zero?

Bad things happen…

>>> e2
Div (Number 10) (Plus (Number 5) (Number (-5)))

>>> runProfile (evalProf e2)
*** Exception: divide by zero
"value: 

Problem: How to get global state AND exception handling ?

Mixing Monads with Transformers

Start with a Basic Monad

m implements

• no special operations

Transform it to add some Capabilities

Transform1 m implements

• m operations and
• operations added by Transform1

Transform again to add more Capabilities

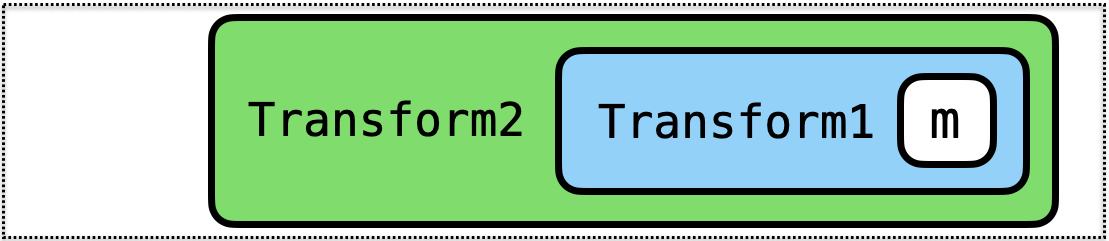
Transform2 (Transform1 m) implements

• m operations and
• operations added by Transform1 and
• operations added by Transform2

… And so on

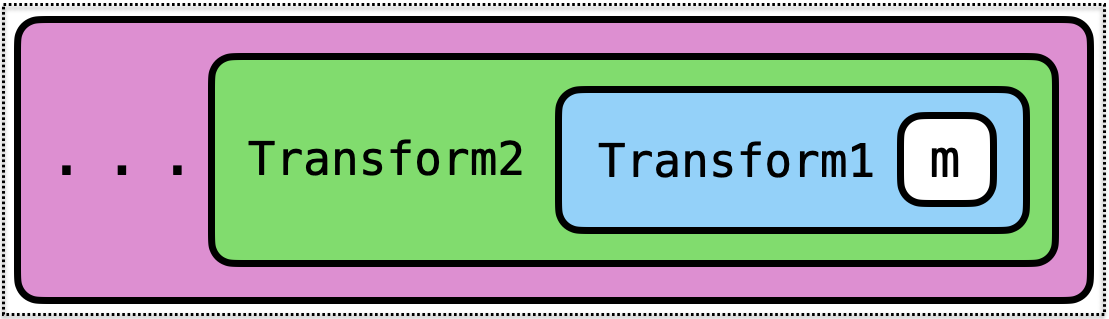
Transform3 (Transform2 (Transform1 m)) implements

• m operations and
• operations added by Transform1 and
• operations added by Transform2 and
• operations added by Transform3 …

Reminiscent of the Decorator Design Pattern or Python’s Decorators.

Mixing Monads with Transformers

• Step 1: Specifying Monads with Extra Features

• Step 2: Implementing Monads with Extra Features

Specifying Monads with Extra Features

First, instead of using concrete monads

• e.g. Profile or Either

We will use type-classes to abstractly specify a monad’s capabilities

• e.g. MonadState s m or MonadError e m

A Class for State-Transformers Monads

The class MonadState s m defined in the Control.Monad.State says

• m is a State-Transformer monad with state type s

class Monad m => MonadState s m where
  get :: m s
  put :: s -> m ()

That is to say, m implements

• >>= and return operations specified by Monad and

• get and put operations specified by MonadState!

Generalize Types to use Classes

So we can generalize the type of count to use MonadState Int m

count :: (MonadState Int m) => m ()
count = do
  n <- get
  put (n+1)

A Class for Exception Handling Monads

The class MonadError e m defined in [Control.Monad.Except][6] says

• m is a Exception-Handling monad with exception type e

class Monad m => MonadError e m where
  throwError :: e -> m a
  catchError :: m a -> (e -> m a) -> m a

That is to say, m implements

• >>= and return operations specified by Monad and

• throwError and catchError operations specified by MonadError!

Generalize Types to use Classes

So we can generalize the type of tryCatch to use MonadError e m

tryCatch :: (MonadError e m) => m a -> a -> m a  
tryCatch m def = catchError m (\_ -> return def)

Generalize eval to use Constraints

We can now specify that eval uses a monad m that implements

• MonadState Int and MonadError Expr

eval :: (MonadState Int m, MonadError Expr m) => Expr -> m Int 
eval (Number n)    = return n
eval (Plus  e1 e2) = do n1 <- eval e1 
                        n2 <- eval e2
                        count
                        return (n1 + n2)
eval (Div   e1 e2) = do n1 <- eval e1 
                        n2 <- eval e2
                        count
                        if (n2 /= 0) 
                          then return (n1 `div` n2) 
                          else throwError e2
eval (Try e n)     = tryCatch (eval e) n

Lets try to run it!

>>> e1

>>> evalMix e1
... GHC yells "please IMPLEMENT this MAGIC monad that implements BOTH features"

Mixing Monads with Transformers

• Step 1: Specifying Monads with Extra Features

• Step 2: Implementing Monads with Extra Features

Implementing Monads with Extra Features

Transform2 (Transform1 m) implements

• m operations and
• operations added by Transform1 and
• operations added by Transform2

We require

• A basic monad m
• A Transform1 that adds State capabilities
• A Transform2 that adds Exception capabilities

A Basic Monad

First, lets make a basic monad

• only implements >>= and return

data Identity a = Id a

instance Monad Identity where
  return a     = Id a
  (Id a) >>= f = f a

A very basic monad: just a wrapper (Id) around the value (a)

• No extra features

A Transform that adds State Capabilities

The transformer StateT s m defined in the Control.Monad.State module - takes as input monad m and

• transforms it into a new monad m'

such that m' implements

• all the operations that m implements

• and adds State-transformer capabilities

StateT s m satisfies the constraint (MonadState s (StateT s m))

A State-transformer over Int states

type Prof = StateT Int Identity 

We can go back and give evalProf the type

evalProf :: Expr -> Prof Int

A Transform that adds Exception Capabilities

The transformer ExceptT e m

• takes as input a monad m and
• transforms it into a new monad m'

such that m' implements

• all the operations that m implements

• and adds Exception-handling capabilities

ExceptT e m satisfies the constraint (MonadError e (ExceptT e m))

An Exception Handler Monad with Expr-typed exceptions

type Exn = ExceptT Expr Identity 

We can go back and give evalThrowCatch the type

evalThrowCatch :: Expr -> Exn Int

Composing Transformers

We can use both transformers to get both powers!

type ExnProf a = ExceptT Expr (StateT Int (Identity)) a

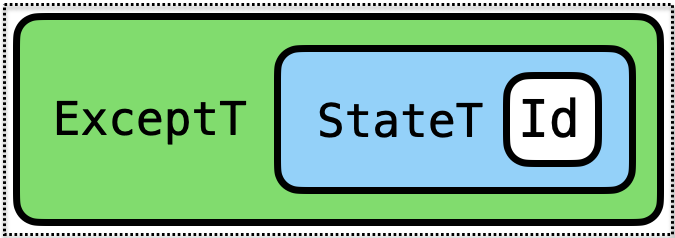
ExnProf implements State-transformer-over Int and Exception-handling-over-Expr

EXERCISE: Executing the Combined Transformer

Recall that

type ExnProf a = ExceptT Expr (StateT Int (Identity)) a

Lets write a function

runExnProf :: (Show a) => ExnProf a -> String
runExnProf epm = ???

such that

>>> runExnProf (eval e1) 
"value: 1, count: 2"

>>> runExnProf (eval e2) 
"Plus (Number 5) (Number (-5)) after 2 operations"

TRY AT HOME: Combining in a Different Order

We can also combine the transformers in a different order

type ProfExn a = StateT Int (ExceptT Expr (Identity)) a

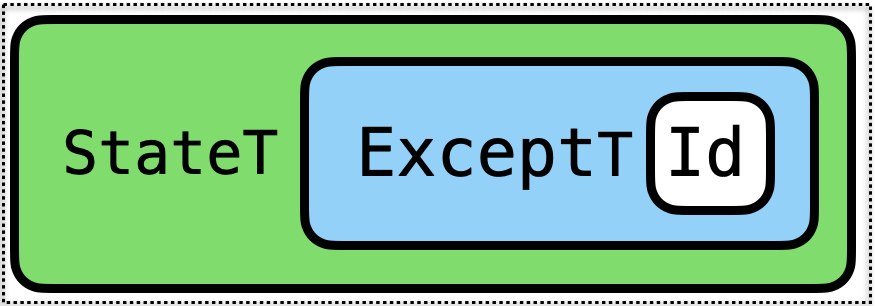
ExnProf implements State-transformer-over Int and Exception-handling-over-Expr

Can you implement the function

runProfExn :: (Show a) => ProfExn a -> String

such that when you are done, we can get the following behavior?

>>> runProfExn (eval e1) 
"value: 1, count: 2"

>>> runProfExn (eval e2) 
"Left (Plus (Number 5) (Number (-5)))"

Summary: Mixing Monads with Many Features

1. Transformers add capabilities to Monads

Transform2 (Transform1 m) implements

• m operations and
• operations added by Transform1 and
• operations added by Transform2

2. StateT and ExceptT add State and Exceptions

• Start with a basic monad Identity
• Use StateT Int to add global-Int state-update capabilities
• Use ExceptT Expr to add exception-handling capabilities

Play around with this in your homework assignment!