Overloading Operators: Arithmetic

The + operator works for a bunch of different types.

For Integer:

λ> 2 + 3
5

for Double precision floats:

λ> 2.9 + 3.5
6.4

Overloading Comparisons

Similarly we can compare different types of values

λ> 2 == 3
False

λ>  [2.9, 3.5] == [2.9, 3.5]
True

λ> ("cat", 10) < ("cat", 2)
False

λ> ("cat", 10) < ("cat", 20)
True

Ad-Hoc Overloading

Seems unremarkable?

Languages since the dawn of time have supported “operator overloading”

• To support this kind of ad–hoc polymorphism

• Ad-hoc: “created or done for a particular purpose as necessary.”

You really need to add and compare values of multiple types!

Haskell has no caste system

No distinction between operators and functions

• All are first class citizens!

But then, what type do we give to functions like + and == ?

QUIZ

Which of the following would be appropriate types for (+) ?

(A) (+) :: Integer -> Integer -> Integer

(B) (+) :: Double -> Double -> Double

(C) (+) :: a -> a -> a

(D) All of the above

(E) None of the above

Integer -> Integer -> Integer is bad because?

• Then we cannot add Doubles!

Double -> Double -> Double is bad because?

• Then we cannot add Doubles!

a -> a -> a is bad because?

• That doesn’t make sense, e.g. to add two Bool or two [Int] or two functions!

Type Classes for Ad Hoc Polymorphism

Haskell solves this problem with typeclasses

• Introduced by Wadler and Blott

BTW: The paper is one of the clearest examples of academic writing I have seen. The next time you hear a curmudgeon say all the best CS was done in the 60s or 70s just point them to the above.

Qualified Types

To see the right type, lets ask:

λ> :type (+)
(+) :: (Num a) => a -> a -> a

We call the above a qualified type. Read it as +

• takes in two a values and returns an a value

for any type a that

• is a Num or
• implements the Num interface or
• is an instance of a Num.

The name Num can be thought of as a predicate or constraint over types.

Some types are Nums

Examples include Integer, Double etc

• Any such values of those types can be passed to +.

Other types are not Nums

Examples include Char, String, functions etc,

• Values of those types cannot be passed to +.

λ> True + False

<interactive>:15:6:
    No instance for (Num Bool) arising from a use of ‘+’
    In the expression: True + False
    In an equation for ‘it’: it = True + False

Aha! Now those no instance for error messages should make sense!

• Haskell is complaining that True and False are of type Bool
• and that Bool is not an instance of Num.

Type Class is a Set of Operations

A typeclass is a collection of operations (functions) that must exist for the underlying type.

• Similar but different to Java interfaces

The Eq Type Class

The simplest typeclass is perhaps, Eq

class  Eq a  where
  (==) :: a -> a -> Bool
  (/=) :: a -> a -> Bool

A type a is an instance of Eq if there are two functions

• == and /=

That determine if two a values are respectively equal or disequal.

The Show Type Class

The typeclass Show requires that instances be convertible to String (which can then be printed out)

class  Show a  where
  show :: a -> String

Indeed, we can test this on different (built-in) types

λ> show 2
"2"

λ> show 3.14
"3.14"

λ> show (1, "two", ([],[],[]))
"(1,\"two\",([],[],[]))"

(Hey, whats up with the funny \"?)

Unshowable Types

When we type an expression into ghci,

• it computes the value,
• then calls show on the result.

Thus, if we create a new type by

data Unshowable = A | B | C

and then create values of the type,

λ> let x = A
λ> :type x
x :: Unshowable

but then we cannot view them

λ> x

<interactive>:1:0:
    No instance for (Show Unshowable)
      arising from a use of `print' at <interactive>:1:0
    Possible fix: add an instance declaration for (Show Unshowable)
    In a stmt of a 'do' expression: print it

and we cannot compare them!

λ> x == x

<interactive>:1:0:
    No instance for (Eq Unshowable)
      arising from a use of `==' at <interactive>:1:0-5
    Possible fix: add an instance declaration for (Eq Unshowable)
    In the expression: x == x
    In the definition of `it': it = x == x

Again, the previously incomprehensible type error message should make sense to you.

Creating Instances

Tell Haskell how to show or compare values of type Unshowable

By creating instances of Eq and Show for that type:

instance Eq Unshowable where
  (==) A A = True           -- True if both inputs are A
  (==) B B = True           -- ...or B
  (==) C C = True           -- .. or C
  (==) _ _ = False          -- otherwise

  (/=) x y = not (x == y)   -- Test if `x == y` and negate result!

EXERCISE

Lets create an instance for Show Unshowable

When you are done we should get the following behavior

>>> x = [A, B, C]
[A, B, C]

Automatic Derivation

We should be able to compare and view Unshowble automatically"

Haskell lets us automatically derive implementations for some standard classes

data Showable = A' | B' | C'
  deriving (Eq, Show) -- tells Haskell to automatically generate instances

Now we have

λ> let x' = A'

λ> :type x'
x' :: Showable

λ> x'
A'

λ> x' == x'
True

λ> x' == B'
False

The Num typeclass

Let us now peruse the definition of the Num typeclass.

λ> :info Num
class (Eq a, Show a) => Num a where
  (+) :: a -> a -> a
  (*) :: a -> a -> a
  (-) :: a -> a -> a
  negate :: a -> a
  abs :: a -> a
  signum :: a -> a
  fromInteger :: Integer -> a

A type a is an instance of (i.e. implements) Num if

1. The type is also an instance of Eq and Show, and
2. There are functions to add, multiply, etc. values of that type.

That is, we can do comparisons and arithmetic on the values.

Standard Typeclass Hierarchy

Haskell comes equipped with a rich set of built-in classes.

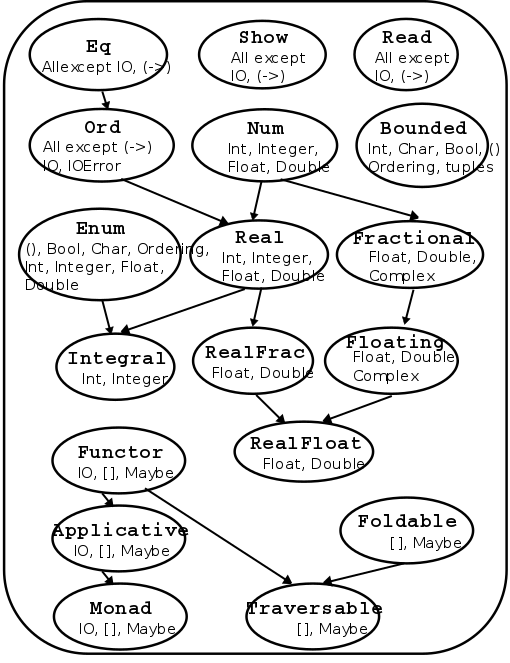
In the above picture, there is an edge from Eq and Show to Num because for something to be a Num it must also be an Eq and Show.

The Ord Typeclass

Another typeclass you’ve used already is the one for Ordering values:

λ> :info (<)
class Eq a => Ord a where
  ...
  (<) :: a -> a -> Bool
  ...

For example:

λ> 2 < 3
True

λ> "cat" < "dog"
True

QUIZ

Recall the datatype:

data Showable = A' | B' | C' deriving (Eq, Show)

What is the result of:

λ> A' < B'

(A) True (B) False (C) Type error (D) Run-time exception

Using Typeclasses

Typeclasses integrate with the rest of Haskell’s type system.

Lets build a small library for Environments mapping keys k to values v

data Table k v
  = Def  v                -- default value `v` to be used for "missing" keys
  | Bind k v (Table k v)  -- bind key `k` to the value `v`
  deriving (Show)

QUIZ

What is the type of keys

keys (Def _)         = []
keys (Bind k _ rest) = k : keys rest

A. Table k v -> k

B. Table k v -> [k]

C. Table k v -> [(k, v)]

D. Table k v -> [v]

E. Table k v -> v

An API for Table

Lets write a small API for Table

-- >>> let env0 = set "cat" 10.0 (set "dog" 20.0 (Def 0))

-- >>> set "cat" env0
-- 10

-- >>> get "dog" env0
-- 20

-- >>> get "horse" env0
-- 0

Ok, lets implement!

-- | 'add key val env' returns a new env that additionally maps `key` to `val`
set :: k -> v -> Table k v -> Table k v
set key val env = ???

-- | 'get key env' returns the value of `key` and the "default" if no value is found
get :: k -> Table k v -> v
get key env = ???

Oops, y u no check?

Constraint Propagation

Lets delete the types of set and get

• to see what Haskell says their types are!

λ> :type get
get :: (Eq k) => k -> v -> Table k v -> Table k v

We can use any k value as a key - if k is an instance of i.e. “implements” the Eq typeclass.

How, did GHC figure this out?

• If you look at the code for get you’ll see that we check if two keys are equal!

HOMEWORK

Write an optimized version of

• set that ensures the keys are in increasing order,
• get that gives up and returns the “default” the moment we see a key thats larger than the one we’re looking for.

(How) do you need to change the type of Table ?

(How) do you need to change the types of get and set ?

Explicit Signatures

Sometimes the use of type classes requires explicit annotations

• which affect the code’s behavior

Read is a standard typeclass that is the “opposite” of Show

• where any instance a ofRead has a “parsing” function

read :: (Read a) => String -> a

QUIZ

What does the expression read "2" evaluate to?

(A) compile time error

(B) "2" :: String

(C) 2 :: Integer

(D) 2.0 :: Double

(E) run-time exception

Compiler is puzzled!

Doesn’t know what type to convert the string to!

Doesn’t know which of the read functions to run!

• Did we want an Int or a Double or maybe something else altogether?

Explicit Type Annotation

• needed to tell Haskell what to convert the string to:

>>> (read "2") :: Int
2

>>> (read "2") :: Float
2.0

Note the different results due to the different types.

Creating Typeclasses

Typeclasses are useful for many different things.

We will see some of those over the next few lectures.

Lets conclude today’s class with a quick example that provides a small taste.

JSON

JavaScript Object Notation or JSON

• is a simple format for transferring data around.

Here is an example:

{ "name"    : "Ranjit"
, "age"     : 44.0
, "likes"   : ["guacamole", "coffee", "tacos"]
, "hates"   : [ "waiting" , "spiders"]
, "lunches" : [ {"day" : "monday",    "loc" : "zanzibar"}
              , {"day" : "tuesday",   "loc" : "farmers market"}
              , {"day" : "wednesday", "loc" : "harekrishna"}
              , {"day" : "thursday",  "loc" : "faculty club"}
              , {"day" : "friday",    "loc" : "coffee cart"} ]
}

In brief, each JSON object is either

• a base value like a string, a number or a boolean,

• an (ordered) array of objects, or

• a set of string-object pairs.

A JSON Datatype

We can represent (a subset of) JSON values with the Haskell datatype

data JVal
  = JStr  String
  | JNum  Double
  | JBool Bool
  | JObj  [(String, JVal)]
  | JArr  [JVal]
  deriving (Eq, Ord, Show)

Thus, the above JSON value would be represented by the JVal

js1 :: JVal
js1 =
  JObj [("name", JStr "Ranjit")
       ,("age",  JNum 44.0)
       ,("likes",   JArr [ JStr "guacamole", JStr "coffee", JStr "bacon"])
       ,("hates",   JArr [ JStr "waiting"  , JStr "grapefruit"])
       ,("lunches", JArr [ JObj [("day",  JStr "monday")
                                ,("loc",  JStr "zanzibar")]
                         , JObj [("day",  JStr "tuesday")
                                ,("loc",  JStr "farmers market")]
                         , JObj [("day",  JStr "wednesday")
                                ,("loc",  JStr "hare krishna")]
                         , JObj [("day",  JStr "thursday")
                                ,("loc",  JStr "faculty club")]
                         , JObj [("day",  JStr "friday")
                                ,("loc",  JStr "coffee cart")]
                         ])
       ]

Serializing Haskell Values to JSON

Lets write a small library to serialize Haskell values as JSON.

We could write a bunch of functions like

doubleToJSON :: Double -> JVal
doubleToJSON = JNum

stringToJSON :: String -> JVal
stringToJSON = JStr

boolToJSON   :: Bool -> JVal
boolToJSON   = JBool

Serializing Collections

But what about collections, namely lists of things?

doublesToJSON    :: [Double] -> JVal
doublesToJSON xs = JArr (map doubleToJSON xs)

boolsToJSON      :: [Bool] -> JVal
boolsToJSON xs   = JArr (map boolToJSON xs)

stringsToJSON    :: [String] -> JVal
stringsToJSON xs = JArr (map stringToJSON xs)

This is getting rather tedious

• We are rewriting the same code :(

Serializing Collections (refactored with HOFs)

You could abstract by making the individual-element-converter a parameter

xsToJSON :: (a -> JVal) -> [a] -> JVal
xsToJSON f xs = JArr (map f xs)

xysToJSON :: (a -> JVal) -> [(String, a)] -> JVal
xysToJSON f kvs = JObj (map (\(k, v) -> (k, f v)) kvs) 

Serializing Collections Still Tedious

As we have to specify the individual data converter (yuck!)

λ> doubleToJSON 4
JNum 4.0

λ> xsToJSON stringToJSON ["coffee", "guacamole", "bacon"]
JArr [JStr "coffee",JStr "guacamole",JStr "bacon"]

λ> xysToJSON stringToJSON [("day", "monday"), ("loc", "zanzibar")]
JObj [("day",JStr "monday"),("loc",JStr "zanzibar")]

This gets awful when you have richer objects like

lunches = [ [("day", "monday"),    ("loc", "zanzibar")]
          , [("day", "tuesday"),   ("loc", "farmers market")]
          ]

because we have to go through gymnastics like

λ> xsToJSON (xysToJSON stringToJSON) lunches
JArr [ JObj [("day",JStr "monday")   ,("loc",JStr "zanzibar")]
     , JObj [("day",JStr "tuesday")  ,("loc",JStr "farmers market")]
     ]

Yikes. So much for readability

Is it too much to ask for a magical toJSON that just works?

Typeclasses To The Rescue

Lets define a typeclass that describes types a that can be converted to JSON.

class JSON a where
  toJSON :: a -> JVal

Now, just make all the above instances of JSON like so

instance JSON Double where
  toJSON = JNum

instance JSON Bool where
  toJSON = JBool

instance JSON String where
  toJSON = JStr

This lets us uniformly write

λ> toJSON 4
JNum 4.0

λ> toJSON True
JBool True

λ> toJSON "guacamole"
JStr "guacamole"

Bootstrapping Instances

Haskell can automatically bootstrap the above to lists and tables!

instance JSON a => JSON [a] where
  toJSON xs = JArr (map toJSON xs)

• if a is an instance of JSON,
• then here’s how to convert lists of a to JSON.

λ> toJSON [True, False, True]
JArr [JBln True, JBln False, JBln True]

λ> toJSON ["cat", "dog", "Mouse"]
JArr [JStr "cat", JStr "dog", JStr "Mouse"]

Bootstrapping Lists of Lists!

λ> toJSON [["cat", "dog"], ["mouse", "rabbit"]]
JArr [JArr [JStr "cat",JStr "dog"],JArr [JStr "mouse",JStr "rabbit"]]

Bootstrapping Key-Value Tables

We can pull the same trick with key-value lists

instance (JSON a) => JSON [(String, a)] where
  toJSON kvs = JObj (map (\(k, v) -> (k, toJSON v)) kvs) 

after which, we are all set!

λ> toJSON lunches
JArr [ JObj [ ("day",JStr "monday"), ("loc",JStr "zanzibar")]
     , JObj [("day",JStr "tuesday"), ("loc",JStr "farmers market")]
     ]

Bootstrapping Tuples

Lets bootstrap the serialization for tuples (upto some fixed size)

instance (JSON a, JSON b) => JSON ((String, a), (String, b)) where
  toJSON ((k1, v1), (k2, v2)) = JObj 
    [ (k1, toJSON v1)
    , (k2, toJSON v2)
    ]

instance (JSON a, JSON b, JSON c) => JSON ((String, a), (String, b), (String, c)) where
  toJSON ((k1, v1), (k2, v2), (k3, v3)) = JObj 
    [ (k1, toJSON v1)
    , (k2, toJSON v2)
    , (k3, toJSON v3)
    ]

instance (JSON a, JSON b, JSON c, JSON d) => JSON ((String, a), (String, b), (String, c), (String,d)) where
  toJSON ((k1, v1), (k2, v2), (k3, v3), (k4, v4)) = JObj 
    [ (k1, toJSON v1)
    , (k2, toJSON v2)
    , (k3, toJSON v3)
    , (k4, toJSON v4)
    ]

instance (JSON a, JSON b, JSON c, JSON d, JSON e) => JSON ((String, a), (String, b), (String, c), (String,d), (String, e)) where
  toJSON ((k1, v1), (k2, v2), (k3, v3), (k4, v4), (k5, v5)) = JObj 
    [ (k1, toJSON v1)
    , (k2, toJSON v2)
    , (k3, toJSON v3)
    , (k4, toJSON v4)
    , (k5, toJSON v5)
    ]

Now, we can simply write

hs = (("name"   , "Ranjit")
     ,("age"    , 41.0)
     ,("likes"  , ["guacamole", "coffee", "bacon"])
     ,("hates"  , ["waiting", "grapefruit"])
     ,("lunches", lunches)
     )

which is a Haskell value that describes our running JSON example, and can convert it directly like so

js2 = toJSON hs

EXERCISE: Serializing Tables

To wrap everything up, lets write a routine to serialize our Table

instance JSON (Table k v) where
  toJSON env = ???

and presto! our serializer just works

>>> env0
Bind "cat" 10.0 (Bind "dog" 20.0 (Def 0))

>>> toJSON env0
JObj [ ("cat", JNum 10.0)
     , ("dog", JNum 20.0)
     , ("def", JNum 0.0)
     ]

Thats it for today.

We will see much more typeclass awesomeness in the next few lectures…