A Tree Datatype
A tree with data at the leaves
data Tree a
= Leaf a
| Node (Tree a) (Tree a)
deriving (Eq, Show)Here’s an example Tree Char
charT :: Tree Char
charT = Node
(Node
(Leaf 'a')
(Leaf 'b'))
(Node
(Leaf 'c')
(Leaf 'a'))
Lets Work it Out!
Write a function to add a distinct label to each leaf
label :: Tree a -> Tree (a, Int)
label = ???such that
>>> label charT
Node
(Node
(Leaf ('a', 0))
(Leaf ('b', 1)))
(Node
(Leaf ('c', 2))
(Leaf ('a', 3)))
Labeling a Tree
label :: Tree a -> Tree (a, Int)
label t = t'
where
(_, t') = (helper 0 t)
helper :: Int -> (Int, Tree (a, Int))
helper n (Leaf x) = (n+1, Leaf (x, n))
helper n (Node l r) = (n'', Node l' r')
where
(n', l') = helper n l
(n'', r') = helper n' r
EXERCISE
Now, modify label so that you get new numbers for each letter so,
>>> keyLabel (Node (Node (Leaf 'a') (Leaf 'b')) (Node (Leaf 'c') (Leaf 'a')))
(Node
(Node (Leaf ('a', 0)) (Leaf ('b', 0)))
(Node (Leaf ('c', 0)) (Leaf ('a', 1))))That is, a separate counter for each key a, b, c etc.
HINT Use the following Map k v type
-- | The empty Map
empty :: Map k v
-- | 'insert key val m` returns a new map that extends 'm'
-- by setting `key` to `val`
insert :: k -> v -> Map k v -> Map k v
-- | 'findWithDefault def key m' returns the value of `key`
-- in `m` or `def` if `key` is not defined
findWithDefault :: v -> k -> Map k v -> v
Common Pattern?
Both the functions have a common “shape”
OldInt -> (NewInt, NewTree)
OldMap -> (NewMap, NewTree)If we generally think of Int and Map Char Int as global state
OldState -> (NewState, NewVal)
State Transformers
Lets capture the above “pattern” as a type
- A State Type
type State = ... -- lets "fix" it to Int for now... - A State Transformer Type
data ST a = STC (State -> (State, a))A state transformer is a function that
- takes as input an old
s :: State - returns as output a new
s' :: Stateand valuev :: a

Executing Transformers
Lets write a function to evaluate an ST a
evalState :: State -> ST a -> a
evalState = ???
QUIZ
What is the value of quiz ?
st :: St [Int]
st = STC (\n -> (n+3, [n, n+1, n+2]))
quiz = evalState 100 stA. 103
B. [100, 101, 102]
C. (103, [100, 101, 102])
D. [0, 1, 2]
E. Type error
Lets Make State Transformer a Monad!
instance Monad ST where
return :: a -> ST a
return = returnST
(>>=) :: ST a -> (a -> ST b) -> ST b
(>>=) = bindST
EXERCISE: Implement returnST!
What is a valid implementation of returnST?
type State = Int
data ST a = STC (State -> (State, a))
returnST :: a -> ST a
returnST = ???
What is returnST doing ?
returnST v is a state transformer that … ???
(Can someone suggest an explanation in English?)
HELP
Now, lets implement bindST!
type State = Int
data ST a = STC (State -> (State, a))
bindST :: ST a -> (a -> ST b) -> ST b
bindST = ???
What is bindST doing ?
bindST v is a state transformer that … ???
(Can someone suggest an explanation in English?)
bindST lets us sequence state transformers
(>>=) :: ST0 a -> (a -> ST0 b) -> ST0 b
sta >>= f = STC (\s ->
let (s', va) = runState sta s
stb = f va
(s'', vb) = runState stb s'
in
(s'', vb)
)
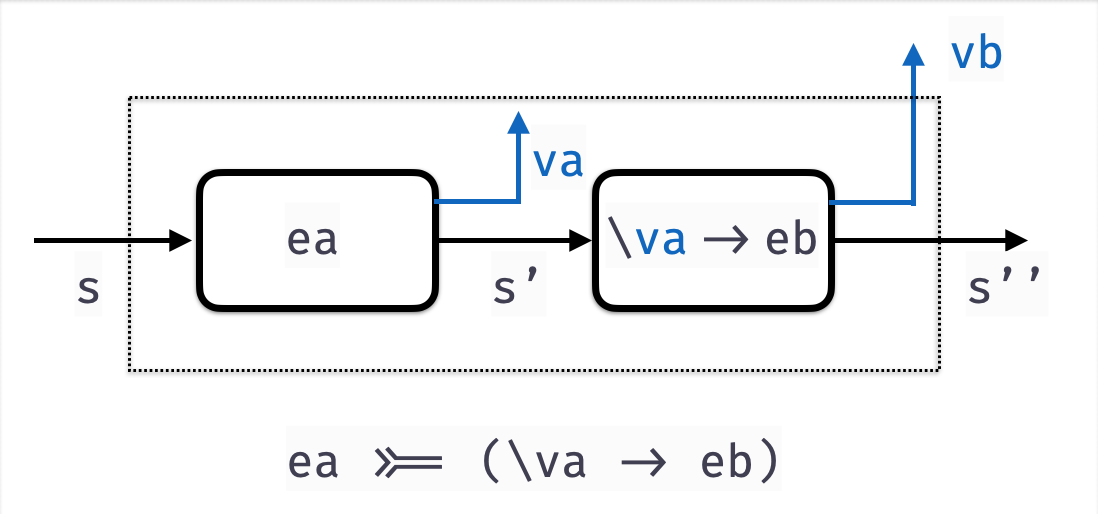
st >>= f
- Applies transformer
stto an initial states- to get output
s'and valueva
- to get output
- Then applies function
fto the resulting valueva- to get a second transformer
- The second transformer is applied to
s'- to get final
s''and valuevb
- to get final
OVERALL: Transform s to s'' and produce value vb
Lets Implement a Global Counter
The (counter) State is an Int
type State = IntA function that increments the counter to return the next Int.
next :: ST String
next = STC (\s -> (s+1, show s))next is a state transformer that that returns String values
QUIZ
Recall that
evalState :: State -> ST a -> a
evalState s (STC st) = snd (st s)
next :: ST String
next = STC (\s -> (s+1, show s))What does quiz evaluate to?
quiz = evalState 100 nextA. "100"
B. "101"
C. "0"
D. "1"
E. (101, "100")
QUIZ
Recall the definitions
evalState :: State -> ST a -> a
evalState s (STC st) = snd (st s)
next :: ST String
next = STC (\s -> (s+1, show s))Now suppose we have
wtf1 = ST String
wtf1 = next >>= \n ->
return nWhat does quiz evaluate to?
quiz = evalState 100 wtf1A. "100"
B. "101"
C. "0"
D. "1"
E. (101, "100")
Example
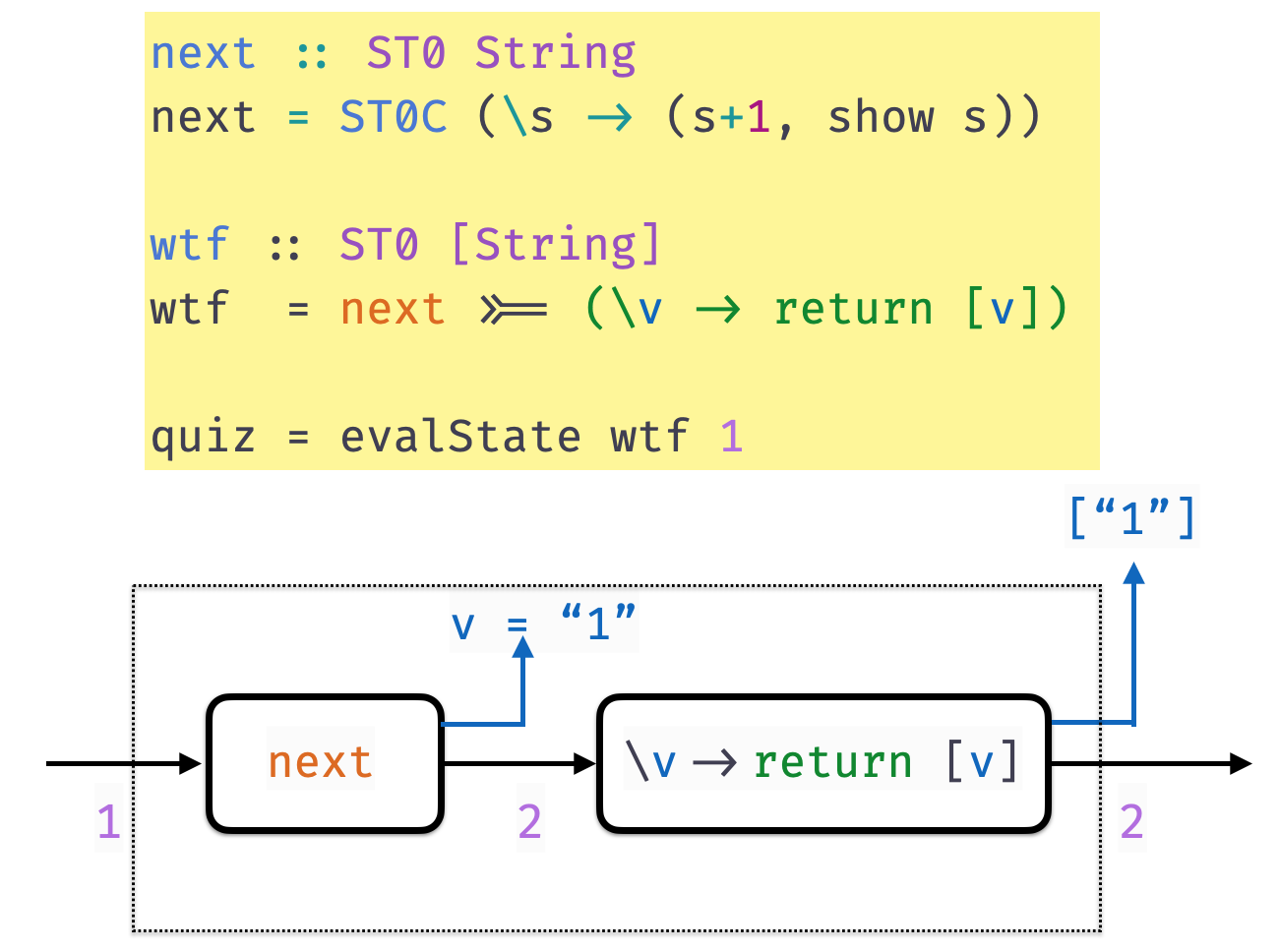
Example
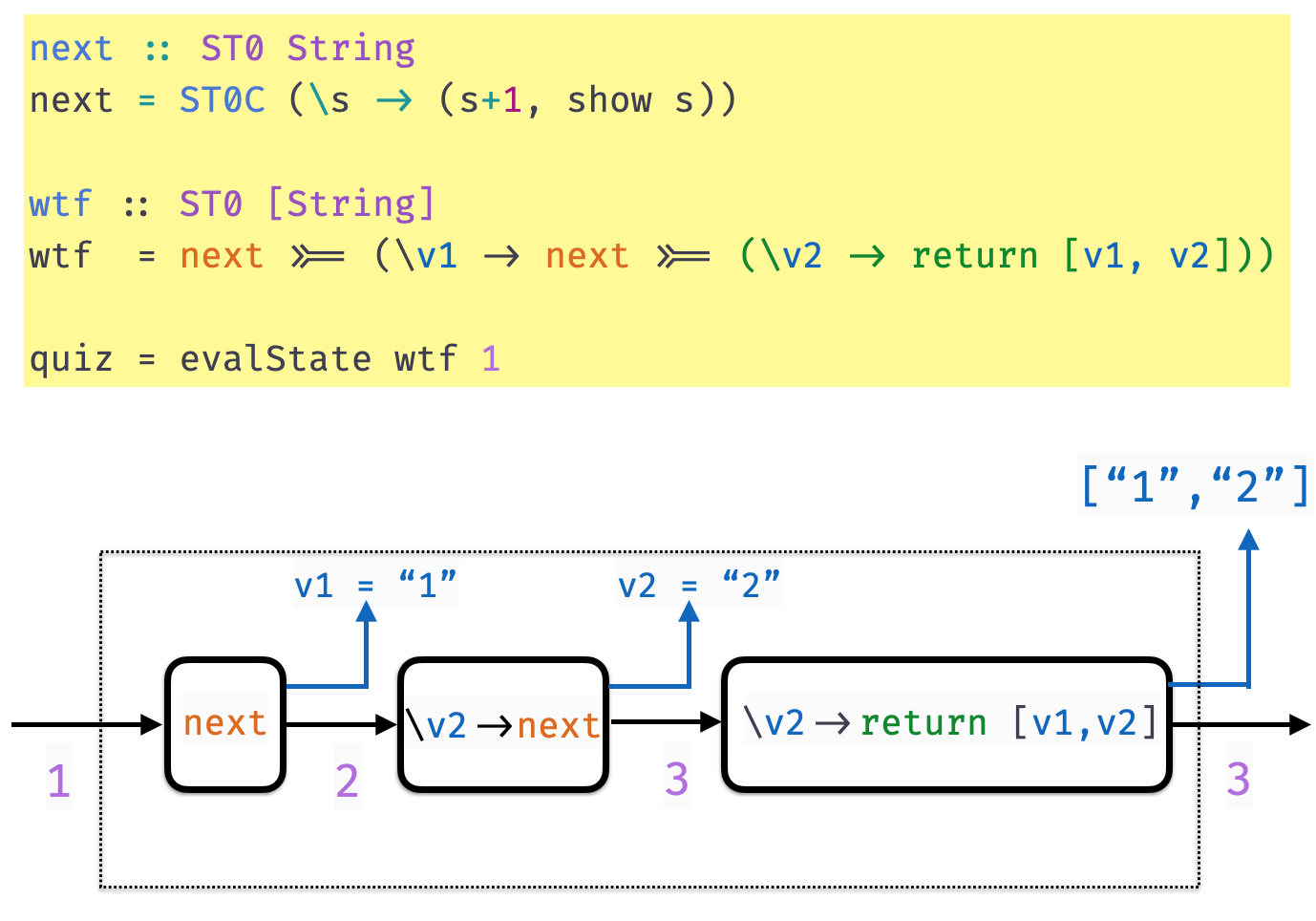
QUIZ
next :: ST String
next = STC (\s -> (s+1, show s)
evalState :: State -> ST a -> a
evalState s (STC f) = snd (f s)Consider a function wtf2 defined as
wtf2 = next >>= \n1 ->
next >>= \n2 ->
next >>= \n3 ->
return [n1, n2, n3]What does quiz evaluate to?
quiz = evalState 100 wtfA. Type Error!
B. [“100”, “100”, “100”]
C. [“0”, “0”, “0”]
D. [“100”, “101”, “102”]
E. [“102”, “102”, “102”]
Chaining Transformers
>>= lets us chain transformers into one big transformer!
So we can define a function to increment the counter by 3
-- Increment the counter by 3
next3 :: ST [Int]
next3 = next >>= \n1 ->
next >>= \n2 ->
next >>= \n3 ->
return [n1,n2,n3]And then sequence it twice to get
next6 :: ST [Int]
next6 = next3 >>= \ns_1_2_3 ->
next3 >>= \ns_4_5_6 ->
return (ns_123 ++ ns_4_5_6)
Lets do the above examples
Remember, do is just nice syntax for the above!
-- Increment the counter by 3
next3 :: ST [String]
next3 = do
n1 <- next
n2 <- next
n3 <- next
return [n1,n2,n3]And then sequence it twice to get
next6 :: ST [String]
next6 = do
ns_123 <- next3
ns_456 <- next3
return (ns_123 ++ ns_4_5_6)
Labeling a Tree with a “Global Counter”
Lets rewrite our Tree labeler with ST
helperS :: Tree a -> ST (Tree (a, Int))
helperS = ???
Wow, compare to the old code!
helper :: Int -> (Int, Tree (a, Int))
helper n (Leaf x) = (n+1, Leaf (x, n))
helper n (Node l r) = (n'', Node l' r')
where
(n', l') = helper n l
(n'', r') = helper n' rAvoid worrying about propagating the “right” counters
- Automatically handled by
STmonad instance!
Executing the Transformer
In the old code we called the helper with an initial counter 0
label :: Tree a -> Tree (a, Int)
label t = t'
where
(_, t') = helper 0 tIn the new code what should we do?
helperS :: Tree a -> ST (Tree (a, Int))
helperS = ...
labelS :: Tree a -> Tree (a, Int)
labelS = ???Now, we should be able to exec the labelS transformer
>>> labelS (Node (Node (Leaf 'a') (Leaf 'b')) (Leaf 'c'))
(Node (Node (Leaf ('a', 0)) (Leaf ('b', 1))) (Leaf ('c', 2)))
How to implement keyLabel?
So far, we hardwired an Int counter as our State
type State = Int
data ST a = STC (State -> (State, a))Have to reimplement the monad if we want a different state?
- e.g.
Map Char Intto implementkeyLabel
Don’t Repeat Yourself!
A Generic State Transformer
Don’t have separate types for IntList and CharList
Define a generic list
[a]whereais a type parameterInstantiate
ato get[Int]and[Char]
Similarly, reuse ST with a type parameter!
data ST s a = STC (s -> (s, a))- State is represented by type
s - Return Value is the type
a(as before).
A Generic State Transformer Monad
Lets make the above a(n instance of) Monad
instance Monad (ST s) where
-- return :: a -> ST s a
return val = ST0C (\s -> (s, val))
-- (>>=) :: ST s a -> (a -> ST s b) -> ST s b
(>>=) sta f = ST0C (\s ->
let (s', va) = runState sta s
stb = f va
(s'', vb) = runState stb s'
in
(s'', vb)
)
runState :: ST s a -> s -> (s, a)
runState (STC f) s = f s
evalState :: ST s a -> s -> a
evalState st s = snd (runState st s) (exactly the same code as returnST and bindST)
Lets implement keyLabel
- Define a
Map Char Intstate-transformer
type CharST a = ST (Map Char Int) a- Modify
nextto take aChar
charNext :: Char -> CharST Int
charNext c = STC (\m ->
let
n = M.findWithDefault 0 c m -- label for 'c'
m' = M.insert c (n+1) m -- update map
in
(m', n)
)- Modify
helperto usecharNext
keyHelperS :: Tree Char -> ST (Tree (Char, Int))
keyHelperS (Leaf c) = do
n <- charNext c
return (Leaf (c, n))
keyHelperS (Node l r) = do
l' <- keyHelperS l
r' <- keyHelperS r
return (Tree l' r')
keyLabelS :: Tree Char -> Tree (Char, Int)
keyLabelS t = evalState (keyHelperS t) empty Lets make sure it works!
>>> keyLabelS charT
Node
(Node (Leaf ('a', 0)) (Leaf ('b', 0)))
(Node (Leaf ('c', 0)) (Leaf ('a', 1)))
Lets look at the final “state”
>>> (final, t) = runState (keyHelper charT) M.emptyThe returned Tree is
>>> t
Node
(Node (Leaf ('a', 0)) (Leaf ('b', 0)))
(Node (Leaf ('c', 0)) (Leaf ('a', 1)))and the final State is
>>> final
fromList [('a',2),('b',1),('c',1)]
Generically Getting and Setting State
As State is “generic”
- i.e. a type variable not
IntorMap Char Intor …
It will be convenient to have “generic” get and put functions
- that read and update the state
-- | `get` leaves state unchanged & returns it as value
get :: ST s s
-- | `set s` changes the state to `s` & returns () as a value
put :: s -> ST s ()
EXERCISE
Can you fill in the implementations of get and set ?
HINT Just follow the types…
-- | `get` leaves state unchanged & returns it as value
get :: ST s s
get = STC (\oldState -> ???)
-- | `put s` changes the state to `s` & returns () as a value
put :: s -> ST s ()
put s = STC (\oldState -> ???)
Using get and put : Global Counter
We can now implement the plain global counter next as
next :: ST Int Int
next = do
n <- get -- save the current counter as 'n'
put (n+1) -- update the counter to 'n+1'
return n -- return the old counter
Using get and put : Frequency Map
Lets implement the char-frequency counter charNext as
charNext :: Char -> ST (Map Char Int) Int
charNext c = do
m <- get -- get current freq-map
let n = M.findWithDefault 0 c m -- current freq for c (or 0)
put (M.insert c (n+1) m) -- update freq for c
return n -- return current as value
A State-Transformer Library
The Control.Monad.State module
defines a State-Transformer like above.
hides the implementation of the transformer
Clients can only use the “public” API
-- | Like 'ST s a' but "private", cannot be directly accessed
data State s a
-- | Like the synonyms described above
get :: State s s
put :: s -> State s ()
runState :: State s a -> s -> (a, s)
evalState :: State s a -> s -> aYour homework will give you practice with using these
- to do imperative functional programming
The IO Monad
Remember the IO a or Recipe a type from this lecture
- Recipes that return a result of type
a - But may also perform some input/output
A number of primitives are provided for building IO recipes
-- IO is a monad
return :: a -> IO a
(>>=) :: IO a -> (a -> IO b) -> IO bBasic actions that can be “chained” via >>= etc.
getChar :: IO Char
putChar :: Char -> IO ()
A Recipe to Read a Line from the Keyboard
getLine :: IO String
getLine = do
x <- getChar
if x == '\n' then
return []
else do
xs <- getLine
return (x:xs)
IO is a “special case” of the State-Transformer
The internal state is a representation of the state of the world
data World -- machine, files, network, internet ...
type IO a = World -> (World, a)A Recipe is a function that
- takes the current
Worldas its argument - returns a value
aand a modifiedWorld
The modified World reflects any input/output done by the Recipe
This is just for understanding, GHC implements IO more efficiently!
