cse230

Monads Can Be Used for Many Things!

Partial Functions
Global Variables
Parsing
Exceptions
Test Generation
Concurrency
…

Exception Handling

Recall our expressions with division

data Expr
  = Number Int            -- ^ 0,1,2,3,4
  | Plus   Expr Expr      -- ^ e1 + e2
  | Div    Expr Expr      -- ^ e1 / e2
  deriving (Show)

We had a potentially crashing evaluator

eval :: Expr -> Int
eval (Number n)    = n
eval (Plus  e1 e2) = eval e1   +   eval e2
eval (Div   e1 e2) = eval e1 `div` eval e2

-- >>> eval (Div (Val 10) (Plus (Number 5) (Number (-5))))
-- Exception: Divide by zero

We defined a `Result` type

data Result a = Ok a | Err String

made it a Monad

instance Monad Result where
  return x      = Ok x
  (Ok v)  >>= f = f v
  (Err s) >>= _ = Err s

and then we can write

eval :: Expr -> Result Int
eval (Number n)    = return n
eval (Plus  e1 e2) = do {n1 <- eval e1; n2 <- eval e2; return (n1   +   n2) } 
eval (Div   e1 e2) = do { n1 <- eval e1; 
                          n2 <- eval e2; 
                          if n2 /= 0 
                            then return (n1 `div` n2) 
                            else Err ("DBZ: " ++ show e2)
                        }

which doesn’t crash but returns an Err

>>> eval (Div (Number 10) (Plus (Number 5) (Number (-5))))
Err "DBZ: Plus (Number 5) (Number (-5))"

and when it succeeds it returns an Ok

>>> eval (Div (Number 10) (Plus (Number 5) (Number (-5))))
Ok 1

Generalizing `Result` to `Either`

The standard library generalizes the Result type to Either

data Result   a = Err String | Ok a 

data Either e a = Left e     | Right a

Err s becomes Left s
Ok v becomes Right v
Result a becomes Either String a

(But we can data other than String in the Left values)

EXERCISE: Generalizing `Result` Monad to `Either` Monad

Lets translate the old Monad instance for Result

instance Monad Result where

  -- return :: a -> Result a
  return x      = Ok x

  -- (>>=) :: Result a -> (a -> Result b) -> Result b
  (Ok v)  >>= f = f v
  (Err s) >>= _ = s

into a Monad instance for Either

instance Monad (Either e) where
  -- return :: a -> Either e a
  return x        = ???

  -- (>>=) :: Either e a -> (a -> Either e b) -> Either e b
  (Right v) >>= f = ???  
  (Left  s) >>= _ = ???

QUIZ

We can rewrite eval to return an Either

eval :: Expr -> Either Expr Int
eval (Number n)    = return n
eval (Plus  e1 e2) = do n1 <- eval e1 
                        n2 <- eval e2
                        return (n1+n2)
eval (Div   e1 e2) = do n1 <- eval e1 
                        n2 <- eval e2
                        if n2 /= 0 
                          then return (n1 `div` n2) 
                          else Left e2

What does quiz evaluate to?

quiz = eval (Div (Val 10) (Plus (Number 5) (Number (-5))))

A. Err "DBZ: Plus (Number 5) (Number (-5))"

B. Left "DBZ: Plus (Number 5) (Number (-5))"

C. Run-time Exception

D. Plus (Number 5) (Number (-5))

E. Left (Plus (Number 5) (Number (-5)))

`Either` is an Exception Monad!

What can you do with exceptions?

throwError an exception (with some value) …
catchError an exception (and use its value) …

1. `throw`ing an Exception

We can simply define

throw :: e -> Either e a
throw exn = Left exn

and now voila

eval :: Expr -> Either Expr Int
eval (Number n)    = return n
eval (Plus  e1 e2) = do n1 <- eval e1 
                        n2 <- eval e2
                        return (n1 + n2)
eval (Div   e1 e2) = do n1 <- eval e1 
                        n2 <- eval e2
                        if n2 /= 0 
                          then return (n1 `div` n2) 
                          else throw e2

Exactly the same evaluator

Result is a Left ==> an exception came all the way to the top.
Either monad ensures the “exception” shoots to the top!

>>> eval (Div (Numer 10) (Plus (Number 5) (Number (-5))))
Left (Minus (Number 5) (Number 5))

No further evaluation happens after a throw because ???

`catch`ing an exception

How to catch an exception?

Lets change our Expr type to

data Expr
  = Number  Int            -- ^ 0,1,2,3,4
  | Plus    Expr Expr      -- ^ e1 + e2
  | Div     Expr Expr      -- ^ e1 / e2
  | Try     Expr Int       -- ^ try e1 n
  deriving (Show)

Informally, try e n evaluates to e but

if e is undefined due to divide-by-zero
then evaluate to n

eval :: Expr -> Either Expr Int
eval (Number n)    = return n
eval (Plus  e1 e2) = do n1 <- eval e1 
                        n2 <- eval e2
                        return (n1+n2)
eval (Div   e1 e2) = do n1 <- eval e1 
                        n2 <- eval e2
                        if n2 /= 0 
                          then return (n1 `div` n2) 
                          else throw e2
eval (Try e n)     = catch (eval e) (\_ -> return n)

QUIZ

What should the type of catch be?

A. Either e a -> (a -> Either e b) -> Either e b

B. Either e a -> (e -> Either e b) -> Either e b

C. Either e a -> (e -> Either e a) -> Either e a

D. Either e a -> Either e a -> Either e a

E. Either e a -> Either e b -> Either e b

Implementing `catch`

Lets implement the catch function!

catch :: Either e a -> (e -> Either e a) -> Either e a
catch (Left  e) handler = ???
catch (Right a) handler = ???

QUIZ

catch :: Either e a -> (e -> Either e a) -> Either e a
catch (Left  e) handle  = ???
catch (Right a) handler = ???

eval :: Expr -> Either Expr Int
eval (Number n)    = return n
eval (Plus  e1 e2) = do n1 <- eval e1 
                        n2 <- eval e2
                        return (n1+n2)
eval (Div   e1 e2) = do n1 <- eval e1 
                        n2 <- eval e2
                        if n2 /= 0 
                          then return (n1 `div` n2) 
                          else throw e2
eval (Try e n)     = catch (eval e) (\_ -> return n)

e1  = Div (Number 10) (Plus (Number 5) (Number (-5)))
e1' = Try e1 7

quiz = eval (Try e1 7)

What does quiz evaluate to?

A. Right 7

B. Left 7

C. Right 0

D. Left 0

E. Left (Plus (Number 5) (Number (-5)))

`Either` is an Exception Monad!

throw an exception (with some value) …
catch an exception (and use its value) …

throw :: e -> Either e a
throw e = Left e

catch :: Either e a -> (e -> Either e a) -> Either e a
catch (Left  e) handle = handle e
catch (Right e) _      = Right  e

Monads Can Be Used for Many Things!

Partial Functions
Global State
Parsing
Exceptions
Test Generation
Concurrency
…

… but what if I want Exceptions and Global State ?

Mixing Monads

What if I want Exceptions and Global State ?

Profiling with the ST Monad

Lets implement a profiling monad that counts the number of operations

-- A State-Transformer with a "global" `Int` counter 
type Profile a = State Int a

We can write a runProfile that

executes the transformer from 0
and renders the result

runProfile :: (Show a) => Profile a -> String 
runProfile st = showValCount (runState st 0)

showValCount :: (Show v, Show c) => (v, c) -> String
showValCount (val, count) = "value: " ++ show val ++ ", count: " ++ show count

A function to increment the counter

count :: Profile ()
count = do
  n <- get
  put (n+1)

A Profiling Evaluator

We can use count to write a profiling evaluator

evalProf :: Expr -> Profile Int 
evalProf = eval 
  where
    eval (Number n)    = return n
    eval (Plus  e1 e2) = do n1 <- eval e1 
                            n2 <- eval e2
                            count
                            return (n1+n2)
    eval (Div   e1 e2) = do n1 <- eval e1 
                            n2 <- eval e2
                            count
                            return (n1 `div` n2)

And now, as there are two operations, we get

>>> e1
Div (Number 10) (Plus (Number 5) (Number 5))

>>> runProfile (evalProf e1)
"value: 1, count: 2"

But what about Divide-by-Zero?

Bad things happen…

>>> e2
Div (Number 10) (Plus (Number 5) (Number (-5)))

>>> runProfile (evalProf e2)
*** Exception: divide by zero
"value:

Problem: How to get global state AND exception handling ?

Mixing Monads with Transformers

Start with a Basic Monad

m implements

no special operations

Transform it to add some Capabilities

Transform1 m implements

m operations and
operations added by Transform1

Transform again to add more Capabilities

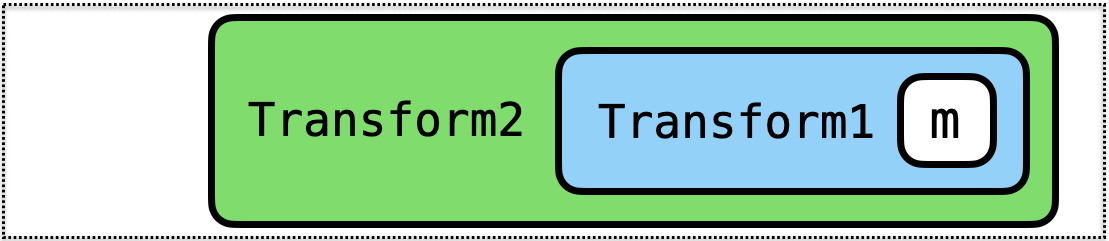
Transform2 (Transform1 m) implements

m operations and
operations added by Transform1 and
operations added by Transform2

… And so on

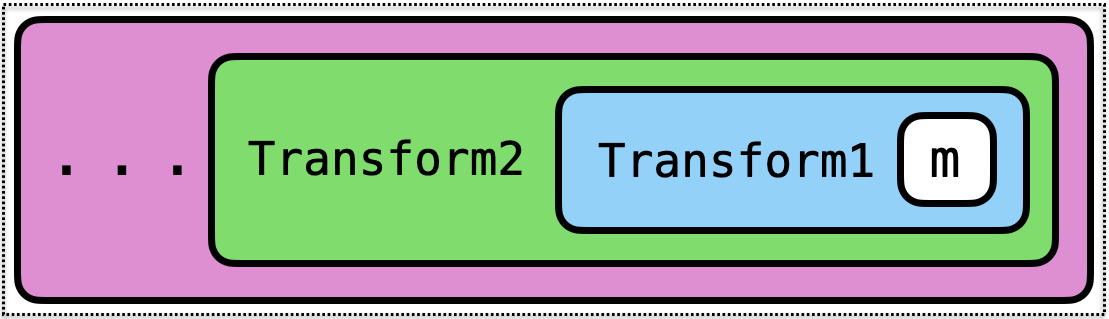
Transform3 (Transform2 (Transform1 m)) implements

m operations and
operations added by Transform1 and
operations added by Transform2 and
operations added by Transform3 …

Reminiscent of the Decorator Design Pattern or Python’s Decorators.

Mixing Monads with Transformers

Step 1: Specifying Monads with Extra Features
Step 2: Implementing Monads with Extra Features

Specifying Monads with Extra Features

First, instead of using concrete monads

e.g. Profile or Either

We will use type-classes to abstractly specify a monad’s capabilities

e.g. MonadState s m or MonadError e m

A Class for State-Transformers Monads

The class MonadState s m defined in the Control.Monad.State says

m is a State-Transformer monad with state type s

class Monad m => MonadState s m where
  get :: m s
  put :: s -> m ()

That is to say, m implements

>>= and return operations specified by Monad and
get and put operations specified by MonadState!

Generalize Types to use Classes

So we can generalize the type of count to use MonadState Int m

count :: (MonadState Int m) => m ()
count = do
  n <- get
  put (n+1)

A Class for Exception Handling Monads

The class MonadError e m defined in [Control.Monad.Except][6] says

m is a Exception-Handling monad with exception type e

class Monad m => MonadError e m where
  throwError :: e -> m a
  catchError :: m a -> (e -> m a) -> m a

That is to say, m implements

>>= and return operations specified by Monad and
throwError and catchError operations specified by MonadError!

Generalize Types to use Classes

So we can generalize the type of tryCatch to use MonadError e m

tryCatch :: (MonadError e m) => m a -> a -> m a  
tryCatch m def = catchError m (\_ -> return def)

Generalize `eval` to use Constraints

We can now specify that eval uses a monad m that implements

MonadState Int and MonadError Expr

eval :: (MonadState Int m, MonadError Expr m) => Expr -> m Int 
eval (Number n)    = return n
eval (Plus  e1 e2) = do n1 <- eval e1 
                        n2 <- eval e2
                        count
                        return (n1 + n2)
eval (Div   e1 e2) = do n1 <- eval e1 
                        n2 <- eval e2
                        count
                        if (n2 /= 0) 
                          then return (n1 `div` n2) 
                          else throwError e2
eval (Try e n)     = tryCatch (eval e) n

Lets try to run it!

>>> e1

>>> evalMix e1
... GHC yells "please IMPLEMENT this MAGIC monad that implements BOTH features"

Mixing Monads with Transformers

Step 1: Specifying Monads with Extra Features
Step 2: Implementing Monads with Extra Features

Implementing Monads with Extra Features

Transform2 (Transform1 m) implements

m operations and
operations added by Transform1 and
operations added by Transform2

We require

A basic monad m
A Transform1 that adds State capabilities
A Transform2 that adds Exception capabilities

A Basic Monad

First, lets make a basic monad

only implements >>= and return

data Identity a = Id a

instance Monad Identity where
  return a     = Id a
  (Id a) >>= f = f a

A very basic monad: just a wrapper (Id) around the value (a)

No extra features

A Transform that adds `State` Capabilities

The transformer StateT s m defined in the Control.Monad.State module - takes as input monad m and

transforms it into a new monad m'

such that m' implements

all the operations that m implements
and adds State-transformer capabilities

StateT s m satisfies the constraint (MonadState s (StateT s m))

A State-transformer over `Int` states

type Prof = StateT Int Identity

We can go back and give evalProf the type

evalProf :: Expr -> Prof Int

A Transform that adds `Except`ion Capabilities

The transformer ExceptT e m

takes as input a monad m and
transforms it into a new monad m'

such that m' implements

all the operations that m implements
and adds Exception-handling capabilities

ExceptT e m satisfies the constraint (MonadError e (ExceptT e m))

An Exception Handler Monad with `Expr`-typed exceptions

type Exn = ExceptT Expr Identity

We can go back and give evalThrowCatch the type

evalThrowCatch :: Expr -> Exn Int

Composing Transformers

We can use both transformers to get both powers!

type ExnProf a = ExceptT Expr (StateT Int (Identity)) a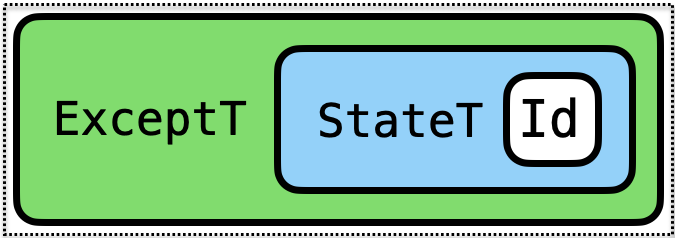

ExnProf implements State-transformer-over Int and Exception-handling-over-Expr

EXERCISE: Executing the Combined Transformer

Recall that

type ExnProf a = ExceptT Expr (StateT Int (Identity)) a

Lets write a function

runExnProf :: (Show a) => ExnProf a -> String
runExnProf epm = ???

such that

>>> runExnProf (eval e1) 
"value: 1, count: 2"

>>> runExnProf (eval e2) 
"Plus (Number 5) (Number (-5)) after 2 operations"

TRY AT HOME: Combining in a Different Order

We can also combine the transformers in a different order

type ProfExn a = StateT Int (ExceptT Expr (Identity)) a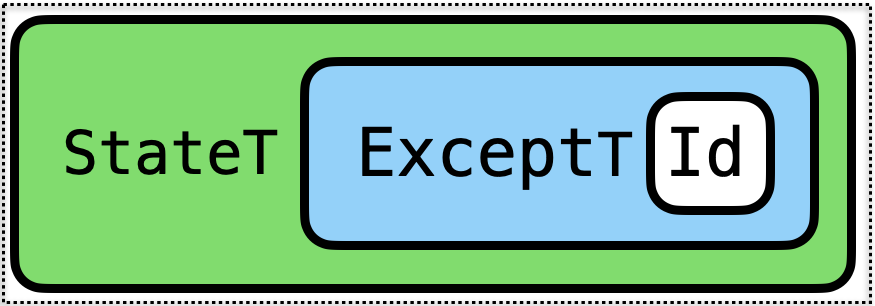

ExnProf implements State-transformer-over Int and Exception-handling-over-Expr

Can you implement the function

runProfExn :: (Show a) => ProfExn a -> String

such that when you are done, we can get the following behavior?

>>> runProfExn (eval e1) 
"value: 1, count: 2"

>>> runProfExn (eval e2) 
"Left (Plus (Number 5) (Number (-5)))"

Summary: Mixing Monads with Many Features

1. Transformers add capabilities to Monads

Transform2 (Transform1 m) implements

m operations and
operations added by Transform1 and
operations added by Transform2

2. `StateT` and `ExceptT` add State and Exceptions

Start with a basic monad Identity
Use StateT Int to add global-Int state-update capabilities
Use ExceptT Expr to add exception-handling capabilities

Play around with this in your homework assignment!

Monads Can Be Used for Many Things!

Exception Handling

We defined a Result type

Generalizing Result to Either

EXERCISE: Generalizing Result Monad to Either Monad

QUIZ

Either is an Exception Monad!

1. throwing an Exception

catching an exception

QUIZ

Implementing catch

QUIZ

Either is an Exception Monad!

Monads Can Be Used for Many Things!

Mixing Monads

Profiling with the ST Monad

A Profiling Evaluator

But what about Divide-by-Zero?

Mixing Monads with Transformers

Start with a Basic Monad

Transform it to add some Capabilities

Transform again to add more Capabilities

… And so on

Mixing Monads with Transformers

Specifying Monads with Extra Features

A Class for State-Transformers Monads

Generalize Types to use Classes

A Class for Exception Handling Monads

Generalize Types to use Classes

Generalize eval to use Constraints

Mixing Monads with Transformers

Implementing Monads with Extra Features

A Basic Monad

A Transform that adds State Capabilities

A State-transformer over Int states

A Transform that adds Exception Capabilities

An Exception Handler Monad with Expr-typed exceptions

Composing Transformers

EXERCISE: Executing the Combined Transformer

TRY AT HOME: Combining in a Different Order

Summary: Mixing Monads with Many Features

1. Transformers add capabilities to Monads

2. StateT and ExceptT add State and Exceptions

We defined a `Result` type

Generalizing `Result` to `Either`

EXERCISE: Generalizing `Result` Monad to `Either` Monad

`Either` is an Exception Monad!

1. `throw`ing an Exception

`catch`ing an exception

Implementing `catch`

`Either` is an Exception Monad!

Generalize `eval` to use Constraints

A Transform that adds `State` Capabilities

A State-transformer over `Int` states

A Transform that adds `Except`ion Capabilities

An Exception Handler Monad with `Expr`-typed exceptions

2. `StateT` and `ExceptT` add State and Exceptions