Polymorphic Functions

doTwice :: (a -> a) -> a -> a 
doTwice f x = f (f x)

Operate on different kinds values

>>> double x = 2 * x
>>> yum x = x ++ " yum! yum!"

>>> doTwice double 10
40
>>> doTwice yum "cookie"
"cookie yum! yum!"

QUIZ

What is the value of quiz?

greaterThan :: Int -> Int -> Bool
greaterThan x y = x > y

quiz = doTwice (greaterThan 10) 0

A. True

B. False

C. Type Error

D. Run-time Exception

E. 101

With great power, comes great responsibility!

>>> doTwice (greaterThan 10) 0 

36:9: Couldn't match type ‘Bool’ with ‘Int’
    Expected type: Int -> Int
      Actual type: Int -> Bool
    In the first argument of ‘doTwice’, namely ‘greaterThan 10’
    In the expression: doTwice (greaterThan 10) 0

The input and output types are different!

Cannot feed the output of (greaterThan 10 0) into greaterThan 10!

Polymorphic Types

But the type of doTwice would have spared us this grief.

>>> :t doTwice
doTwice :: (a -> a) -> a -> a

The signature has a type parameter t

• re-use doTwice to increment Int or concat String or …

• The first argument f must take input t and return output t (i.e. t -> t)

• The second argument x must be of type t

• Then f x will also have type t … and we can call f (f x).

But function is incompatible with doTwice

• if its input and output types differ

QUIZ

Lets make sure you’re following!

What is the type of quiz?

quiz x f = f x

A. a -> a

B. (a -> a) -> a

C. a -> b -> a -> b

D. a -> (a -> b) -> b

E. a -> b -> a

QUIZ

Lets make sure you’re following!

What is the value of quiz?

apply x f = f x

greaterThan :: Int -> Int -> Bool
greaterThan x y = x > y

quiz = apply 100 (greaterThan 10)

A. Type Error

B. Run-time Exception

C. True

D. False

E. 110

Polymorphic Data Structures

Today, lets see polymorphic data types

which contain many kinds of values.

Recap: Data Types

Recall that Haskell allows you to create brand new data types

data Shape 
  = MkRect  Double Double 
  | MkPoly [(Double, Double)]

QUIZ

What is the type of MkRect ?

data Shape 
  = MkRect  Double Double 
  | MkPoly [(Double, Double)]

a. Shape

b. Double

c. Double -> Double -> Shape

d. (Double, Double) -> Shape

e. [(Double, Double)] -> Shape

Tagged Boxes

Values of this type are either two doubles tagged with Rectangle

>>> :type (Rectangle 4.5 1.2)
(Rectangle 4.5 1.2) :: Shape

or a list of pairs of Double values tagged with Polygon

ghci> :type (Polygon [(1, 1), (2, 2), (3, 3)])
(Polygon [(1, 1), (2, 2), (3, 3)]) :: Shape

Data values inside special Tagged Boxes

Recursive Data Types

We can define datatypes recursively too

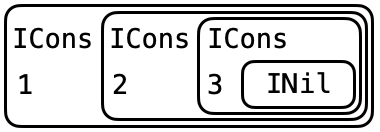
data IntList 
  = INil                -- ^ empty list
  | ICons Int IntList   -- ^ list with "hd" Int and "tl" IntList
  deriving (Show)

(Ignore the bit about deriving for now.)

QUIZ

data IntList 
  = INil                -- ^ empty list
  | ICons Int IntList   -- ^ list with "hd" Int and "tl" IntList
  deriving (Show)

What is the type of ICons ?

A. Int -> IntList -> List

B. IntList

C. Int -> IntList -> IntList

D. Int -> List -> IntList

E. IntList -> IntList

Constructing IntList

Can only build IntList via constructors.

>>> :type INil 
INil:: IntList

>>> :type ICons
ICons :: Int -> IntList -> IntList

EXERCISE

Write down a representation of type IntList of the list of three numbers 1, 2 and 3.

list_1_2_3 :: IntList
list_1_2_3 = ???

Hint Recursion means boxes within boxes

Trees: Multiple Recursive Occurrences

We can represent Int trees like

data IntTree 
   = ILeaf Int              -- ^ single "leaf" w/ an Int
   | INode IntTree IntTree  -- ^ internal "node" w/ 2 sub-trees
   deriving (Show)

A leaf is a box containing an Int tagged ILeaf e.g.

>>> it1  = ILeaf 1 
>>> it2  = ILeaf 2

A node is a box containing two sub-trees tagged INode e.g.

>>> itt   = INode (ILeaf 1) (ILeaf 2)
>>> itt'  = INode itt itt
>>> INode itt' itt'
INode (INode (ILeaf 1) (ILeaf 2)) (INode (ILeaf 1) (ILeaf 2))

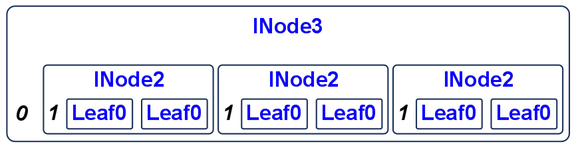
Multiple Branching Factors

e.g. 2-3 trees

data Int23T 
  = ILeaf0 
  | INode2 Int Int23T Int23T
  | INode3 Int Int23T Int23T Int23T
  deriving (Show)

An example value of type Int23T would be

i23t :: Int23T
i23t = INode3 0 t t t
  where t = INode2 1 ILeaf0 ILeaf0

which looks like

Parameterized Types

We can define CharList or DoubleList - versions of IntList for Char and Double as

data CharList 
  = CNil
  | CCons Char CharList
  deriving (Show)

data DoubleList 
   = DNil
   | DCons Char DoubleList
   deriving (Show)

Don’t Repeat Yourself!

Don’t repeat definitions - Instead reuse the list structure across all types!

Find abstract data patterns by

• identifying the different parts and
• refactor those into parameters

A Refactored List

Here are the three types: What is common? What is different?

data IList = INil | ICons Int    IList

data CList = CNil | CCons Char   CList

data DList = DNil | DCons Double DList

Common: Nil/Cons structure

Different: type of each “head” element

Refactored using Type Parameter

data List a = Nil | Cons a  (List a)

Recover original types as instances of List

type IntList    = List Int
type CharList   = List Char
type DoubleList = List Double

Polymorphic Data has Polymorphic Constructors

Look at the types of the constructors

>>> :type Nil 
Nil :: List a

That is, the Empty tag is a value of any kind of list, and

>>> :type Cons 
Cons :: a -> List a -> List a

Cons takes an a and a List a and returns a List a.

cList :: List Char     -- list where 'a' = 'Char' 
cList = Cons 'a' (Cons 'b' (Cons 'c' Nil))

iList :: List Int      -- list where 'a' = 'Int' 
iList = Cons 1 (Cons 2 (Cons 3 Nil))

dList :: List Double   -- list where 'a' = 'Double' 
dList = Cons 1.1 (Cons 2.2 (Cons 3.3 Nil))

Polymorphic Function over Polymorphic Data

Lets write the list length function

len :: List a -> Int
len Nil         = 0
len (Cons x xs) = 1 + len xs

len doesn’t care about the actual values in the list - only “counts” the number of Cons constructors

Hence len :: List a -> Int

• we can call len on any kind of list.

>>> len [1.1, 2.2, 3.3, 4.4]    -- a := Double  
4

>>> len "mmm donuts!"           -- a := Char
11

>>> len [[1], [1,2], [1,2,3]]   -- a := ???
3

Built-in Lists?

This is exactly how Haskell’s “built-in” lists are defined:

data [a]    = [] | (:) a [a]

data List a = Nil | Cons a (List a)

• Nil is called []
• Cons is called :

Many list manipulating functions e.g. in [Data.List][1] are polymorphic - Can be reused across all kinds of lists.

(++) :: [a] -> [a] -> [a]
head :: [a] -> a
tail :: [a] -> [a]

Generalizing Other Data Types

Polymorphic trees

data Tree a 
   = Leaf a 
   | Node (Tree a) (Tree a) 
   deriving (Show)

Polymorphic 2-3 trees

data Tree23 a 
   = Leaf0  
   | Node2 (Tree23 a) (Tree23 a)
   | Node3 (Tree23 a) (Tree23 a) (Tree23 a)
   deriving (Show)

Kinds

List a corresponds to lists of values of type a.

If a is the type parameter, then what is List?

A type-constructor that - takes as input a type a - returns as output the type List a

But wait, if List is a type-constructor then what is its “type”?

• A kind is the “type” of a type.

>>> :kind Int
Int :: *
>>> :kind Char
Char :: *
>>> :kind Bool
Bool :: *

Thus, List is a function from any “type” to any other “type”, and so

>>> :kind List
List :: * -> *

QUIZ

What is the kind of ->? That, is what does GHCi say if we type

>>> :kind (->) 

A. *

B. * -> *

C. * -> * -> *

We will not dwell too much on this now.

As you might imagine, they allow for all sorts of abstractions over data.

If interested, see this for more information about kinds.