A Tree Datatype

A tree with data at the leaves

data Tree a
    = Leaf a
    | Node (Tree a) (Tree a)
    deriving (Eq, Show)

Here’s an example Tree Char

charT :: Tree Char
charT = Node 
            (Node 
                (Leaf 'a') 
                (Leaf 'b')) 
            (Node 
                (Leaf 'c') 
                (Leaf 'a'))

Lets Work it Out!

Write a function to add a distinct label to each leaf

label :: Tree a -> Tree (a, Int)
label = ???

such that

>>> label charT 
Node 
    (Node 
        (Leaf ('a', 0)) 
        (Leaf ('b', 1))) 
    (Node 
        (Leaf ('c', 2)) 
        (Leaf ('a', 3)))

Labeling a Tree

label :: Tree a -> Tree (a, Int)
label t       = t'
  where 
      (_, t') = (helper 0 t)

helper :: Int -> (Int, Tree (a, Int))
helper n (Leaf x)   = (n+1, Leaf (x, n))
helper n (Node l r) = (n'', Node l' r')
  where 
      (n', l')      = helper n l
      (n'', r')     = helper n' r

EXERCISE

Now, modify label so that you get new numbers for each letter so,

>>> keyLabel (Node (Node (Leaf 'a') (Leaf 'b')) (Node (Leaf 'c') (Leaf 'a')))
    (Node
        (Node (Leaf ('a', 0)) (Leaf ('b', 0))) 
        (Node (Leaf ('c', 0)) (Leaf ('a', 1))))

That is, a separate counter for each key a, b, c etc.

HINT Use the following Map k v type

-- | The empty Map
empty :: Map k v

-- | 'insert key val m` returns a new map that extends 'm'
--   by setting `key` to `val`
insert :: k -> v -> Map k v -> Map k v

-- | 'findWithDefault def key m' returns the value of `key`
--   in `m`  or `def` if `key` is not defined
findWithDefault :: v -> k -> Map k v -> v

Common Pattern?

Both the functions have a common “shape”

    OldInt -> (NewInt, NewTree)

    OldMap -> (NewMap, NewTree)

If we generally think of Int and Map Char Int as global state

    OldState -> (NewState, NewVal)

State Transformers

Lets capture the above “pattern” as a type

1. A State Type

type State = ... -- lets "fix" it to Int for now... 

2. A State Transformer Type

data ST a = STC (State -> (State, a))

A state transformer is a function that

• takes as input an old s :: State
• returns as output a new s' :: State and value v :: a

Executing Transformers

Lets write a function to evaluate an ST a

evalState:: State -> ST a -> a
evalState= ???

QUIZ

What is the value of quiz ?

st :: St [Int]
st = STC (\n -> (n+3, [n, n+1, n+2]))

quiz = evalState100 st

A. 103

B. [100, 101, 102]

C. (103, [100, 101, 102])

D. [0, 1, 2]

E. Type error

Lets Make State Transformer a Monad!

instance Monad ST where
    return :: a -> ST a
    return = returnST

    (>>=)  :: ST a -> (a -> ST b) -> ST b
    (>>=) = bindST

EXERCISE: Implement returnST!

What is a valid implementation of returnST?

type State = Int
data ST a  = STC (State -> (State, a))

returnST :: a -> ST a
returnST = ???

What is returnST doing ?

returnST v is a state transformer that … ???

(Can someone suggest an explanation in English?)

HELP

Now, lets implement bindST!

type State = Int

data ST a  = STC (State -> (State, a))

bindST :: ST a -> (a -> ST b) -> ST b
bindST = ???

What is returnST doing ?

returnST v is a state transformer that … ???

(Can someone suggest an explanation in English?)

What is returnST doing ?

returnST v is a state transformer that … ???

(Can someone suggest an explanation in English?)

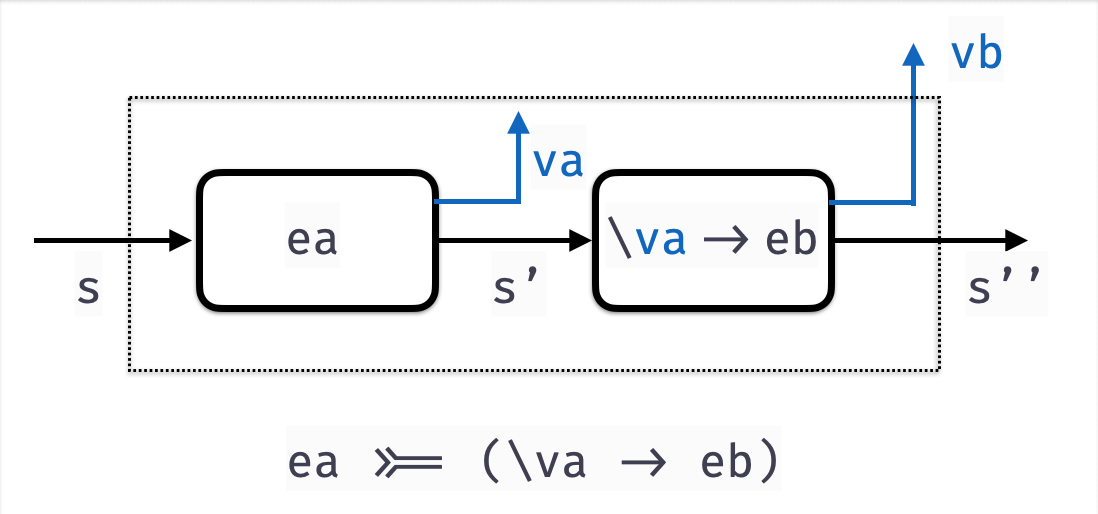
bindST lets us sequence state transformers

(>>=) :: ST0 a -> (a -> ST0 b) -> ST0 b
sta >>= f = STC (\s -> 
                    let (s', va)  = runState sta s 
                        stb       = f va
                        (s'', vb) = runState stb s'
                    in 
                        (s'', vb)
                )

st >>= f

1. Applies transformer st to an initial state s
   • to get output s' and value va
2. Then applies function f to the resulting value va
   • to get a second transformer
3. The second transformer is applied to s'
   • to get final s'' and value vb

OVERALL: Transform s to s'' and produce value vb

Lets Implement a Global Counter

The (counter) State is an Int

type State = Int

A function that increments the counter to return the next Int.

next :: ST String
next = STC (\s -> (s+1, show s))

next is a state transformer that that returns String values

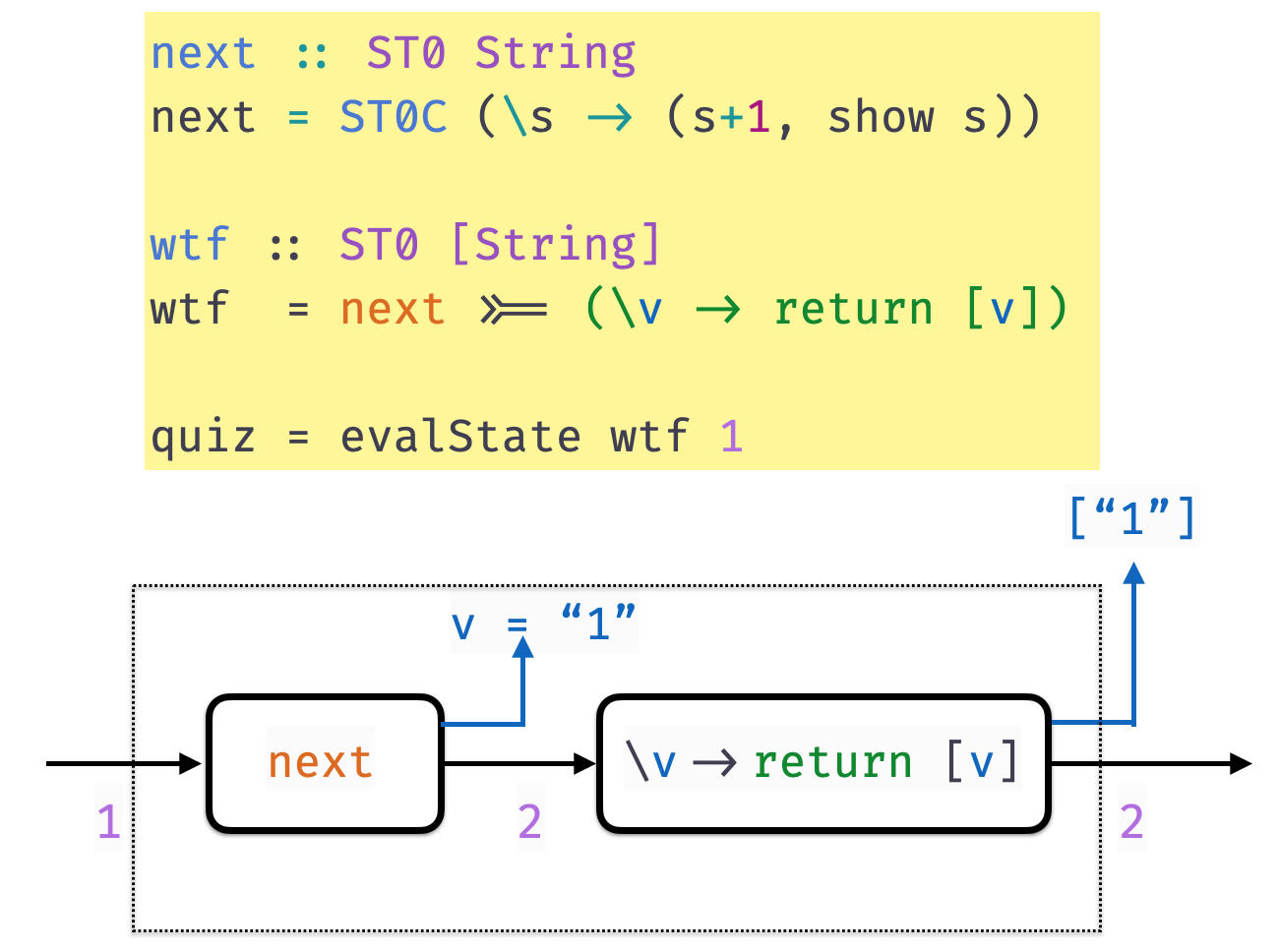
QUIZ

Recall that

evalState :: State -> ST a -> a
evalState s (STC st) = snd (st s)

next :: ST String
next = STC (\s -> (s+1, show s))

What does quiz evaluate to?

quiz = evalState 100 next

A. "100"

B. "101"

C. "0"

D. "1"

E. (101, "100")

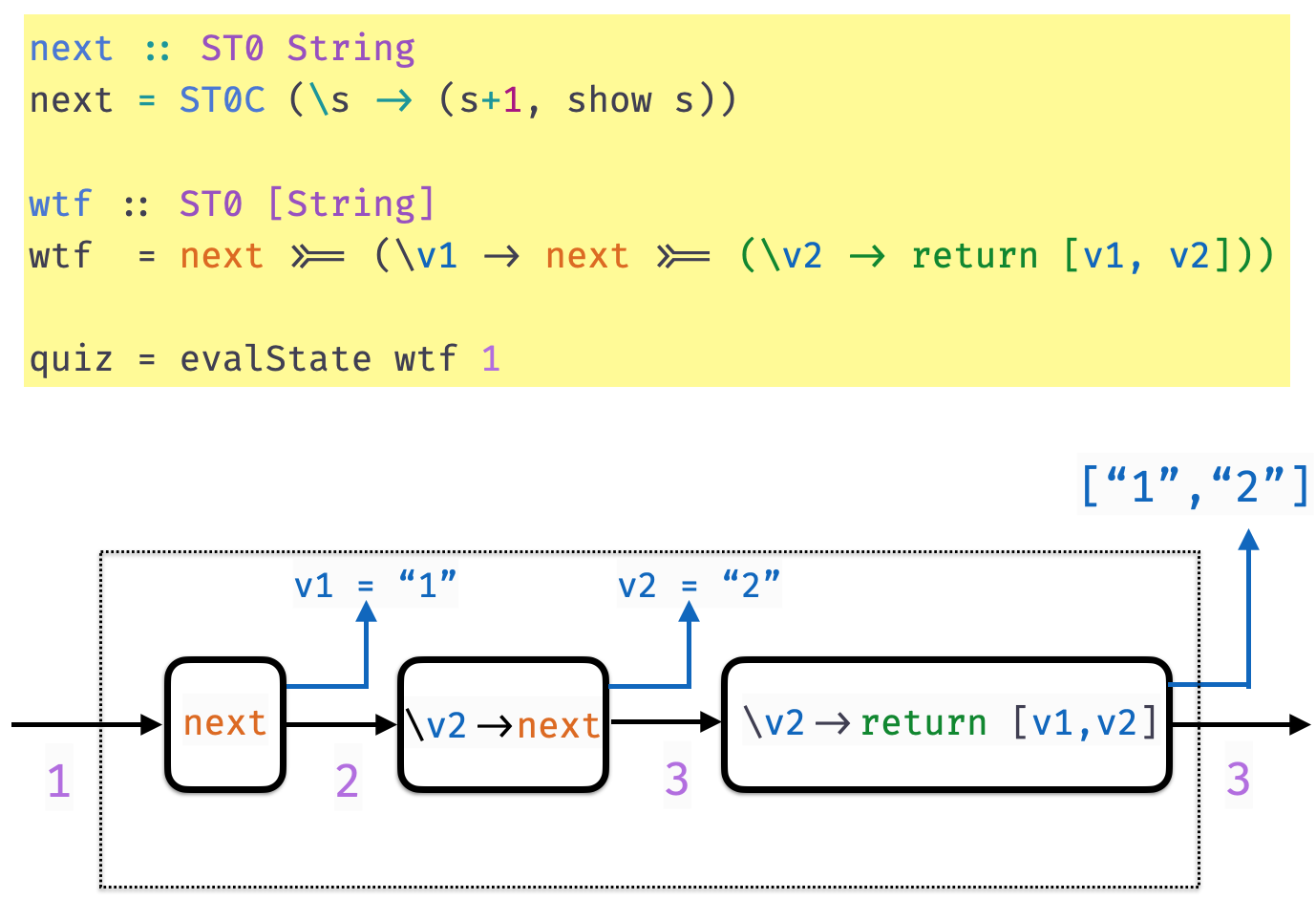
QUIZ

Recall the definitions

evalState :: State -> ST a -> a
evalState s (STC st) = snd (st s)

next :: ST String
next = STC (\s -> (s+1, show s))

Now suppose we have

wtf1 = ST Int
wtf1 = next >>= \n ->
         return n

What does quiz evaluate to?

quiz = evalState 100 wtf1

A. 100

B. 101

C. 0

D. 1

E. (101, 100)

Example

Riyadh Moosa

Example

QUIZ

Consider a function wtf2 defined as

wtf2 = next >>= \n1 ->
         next >>= \n2 ->
           next >>= \n3 ->
             return [n1, n2, n3]

What does quiz evaluate to?

quiz = evalState 100 wtf

A. Type Error!

B. [100, 100, 100]

C. [0, 0, 0]

D. [100, 101, 102]

E. [102, 102, 102]

Chaining Transformers

>>= lets us chain transformers into one big transformer!

So we can define a function to increment the counter by 3

-- Increment the counter by 3
next3 :: ST [Int, Int]
next3 = next >>= \n1 ->
          next >>= \n2 ->
            next >>= \n3 ->
                return [n1,n2,n3]

And then sequence it twice to get

next6 :: ST [Int]
next6 = next3 >>= \ns_1_2_3 ->
          next3 >>= \ns_4_5_6 ->
            return (ns_123 ++ ns_4_5_6)

Lets do the above examples

Remember, do is just nice syntax for the above!

-- Increment the counter by 3
next3 :: ST [Int, Int]
next3 = do
  n1 <- next
  n2 <- next
  n3 <- next
  return [n1,n2,n3]

And then sequence it twice to get

next6 :: ST [Int]
next6 = do
  ns_123 <- next3
  ns_456 <- next3
  return (ns_123 ++ ns_4_5_6)

Labeling a Tree with a “Global Counter”

Lets rewrite our Tree labeler with ST

helperS :: Tree a -> ST (Tree (a, Int))
helperS = ???

Wow, compare to the old code!

helper :: Int -> (Int, Tree (a, Int))
helper n (Leaf x)   = (n+1, Leaf (x, n))
helper n (Node l r) = (n'', Node l' r')
  where 
      (n', l')      = helper n l
      (n'', r')     = helper n' r

Avoid worrying about propagating the “right” counters

• Automatically handled by ST monad instance!

Executing the Transformer

In the old code we called the helper with an initial counter 0

label :: Tree a -> Tree (a, Int)
label t       = t'
  where
      (_, t') = helper 0 t

In the new code what should we do?

helperS :: Tree a -> ST (Tree (a, Int))
helperS = ...

labelS :: Tree a -> Tree (a, Int)
labelS = ???

Now, we should be able to exec the labelS transformer

>>> labelS (Node (Node (Leaf 'a') (Leaf 'b')) (Leaf 'c'))
(Node (Node (Leaf ('a', 0)) (Leaf ('b', 1))) (Leaf ('c', 2)))

How to implement keyLabel?

So far, we hardwired an Int counter as our State

type State = Int

data ST a  = STC (State -> (State, a))

Have to reimplement the monad if we want a different state?

• e.g. Map Char Int to implement keyLabel

Don’t Repeat Yourself!

A Generic State Transformer

Don’t have separate types for IntList and CharList

• Define a generic list [a] where a is a type parameter

• Instantiate a to get [Int] and [Char]

Similarly, reuse ST with a type parameter!

data ST s a = STC (s -> (s, a))

• State is represented by type s
• Return Value is the type a (as before).

A Generic State Transformer Monad

Lets make the above a(n instance of) Monad

instance Monad (ST s) where
  -- return :: a -> ST s a
  return val = ST0C (\s -> (s, val)) 

  -- (>>=) :: ST s a -> (a -> ST s b) -> ST s b
  (>>=) sta f = ST0C (\s -> 
                       let (s', va)  = runState sta s 
                           stb       = f va
                           (s'', vb) = runState stb s'
                       in 
                           (s'', vb)
                     )

runState :: ST s a -> s -> (s, a)
runState (STC f) s = f s

evalState :: ST s a -> s -> a
evalState st s = snd (runState st s) 

(exactly the same code as returnST and bindST)

Lets implement keyLabel

1. Define a Map Char Int state-transformer

type CharST a = ST (Map Char Int) a

2. Modify next to take a Char

charNext :: Char -> CharST Int
charNext c = STC (\m -> 
    let 
        n  = M.findWithDefault 0 c m    -- label for 'c' 
        m' = M.insert c (n+1) m         -- update map
    in 
        (m', n)
    )

3. Modify helper to use charNext

keyHelperS :: Tree Char -> ST (Tree (Char, Int))
keyHelperS (Leaf c) = do 
    n <- charNext c
    return (Leaf (c, n))

keyHelperS (Node l r) = do
    l' <- keyHelperS l
    r' <- keyHelperS r
    return (Tree l' r')

keyLabelS :: Tree Char -> Tree (Char, Int)
keyLabelS t = evalState (keyHelperS t) empty 

Lets make sure it works!

>>> keyLabelS charT
Node
    (Node (Leaf ('a', 0)) (Leaf ('b', 0))) 
    (Node (Leaf ('c', 0)) (Leaf ('a', 1)))

Lets look at the final “state”

>>> (final, t) = runState (keyHelper charT) M.empty

The returned Tree is

>>> t
Node
    (Node (Leaf ('a', 0)) (Leaf ('b', 0))) 
    (Node (Leaf ('c', 0)) (Leaf ('a', 1)))

and the final State is

>>> final
fromList [('a',2),('b',1),('c',1)]

Generically Getting and Setting State

As State is “generic”

• i.e. a type variable not Int or Map Char Int or …

It will be convenient to have “generic” get and put functions

• that read and update the state

-- | `get` leaves state unchanged & returns it as value
get :: ST s s

-- | `set s` changes the state to `s` & returns () as a value
put :: s -> ST s ()

EXERCISE

Can you fill in the implementations of get and set ?

HINT Just follow the types…

-- | `get` leaves state unchanged & returns it as value
get :: ST s s
get = STC (\oldState -> ???) 

-- | `put s` changes the state to `s` & returns () as a value
put :: s -> ST s ()
put s = STC (\oldState -> ???)

Using get and put : Global Counter

We can now implement the plain global counter next as

next :: ST Int Int
next = do 
    n <- get     -- save the current counter as 'n'
    put (n+1)    -- update the counter to 'n+1'
    return n     -- return the old counter

Using get and put : Frequency Map

Lets implement the char-frequency counter charNext as

charNext :: Char -> ST (Map Char Int) Int
charNext c = do
  m    <- get                      -- get current freq-map
  let n = M.findWithDefault 0 c m  -- current freq for c (or 0)
  put (M.insert c (n+1) m)         -- update freq for c
  return n                         -- return current as value

A State-Transformer Library

The Control.Monad.State module

• defines a State-Transformer like above.

• hides the implementation of the transformer

Clients can only use the “public” API

-- | Like 'ST s a' but "private", cannot be directly accessed
data State s a 

-- | Like the synonyms described above
get       :: State s s 
put       :: s -> State s () 
runState  :: State s a -> s -> (a, s)
evalState :: State s a -> s -> a

Your homework will give you practice with using these

• to do imperative functional programming

The IO Monad

Remember the IO a or Recipe a type from this lecture

• Recipes that return a result of type a
• But may also perform some input/output

A number of primitives are provided for building IO recipes

-- IO is a monad
return  :: a -> IO a
(>>=)   :: IO a -> (a -> IO b) -> IO b

Basic actions that can be “chained” via >>= etc.

getChar :: IO Char
putChar :: Char -> IO ()

A Recipe to Read a Line from the Keyboard

getLine :: IO String
getLine =  do 
  x <- getChar
  if x == '\n' then 
      return []
  else do 
      xs <- getLine
      return (x:xs)

IO is a “special case” of the State-Transformer

The internal state is a representation of the state of the world

data World -- machine, files, network, internet ... 

type IO a  = World -> (World, a)

A Recipe is a function that

• takes the current World as its argument
• returns a value a and a modified World

The modified World reflects any input/output done by the Recipe

This is just for understanding, GHC implements IO more efficiently!