import Cse230wi25.BigStep
set_option pp.fieldNotation false
set_option pp.proofs true
Axiomatic Semantics
The BigStep semantics that was saw previously was helpful in proving properties
about groups of programs, for example, that
- that every command
cwas deterministic or - that every command
cwas equivalent toSKIP ;; corIF cond THEN c ELSE cor - that every command
x <~ a;; y <~ awas equivalent tox <~ a;; y <~ x(ifxwas not read ina).
Next, lets try to use the BigStep semantics to check properties of individual programs.
Example: Swapping two Variables
Consider the following Com program that swaps
the values of x and y using z as a temporary
storage.
open Aexp
def swap :=
-- {{ y = b /\ x = a }}
z <~ var x ;;
-- {{ y = b /\ z = a }}
x <~ var y ;;
-- {{ x = b /\ z = a }}
y <~ var z
-- {{ x = b /\ y = a }}
theorem swap_ok : ∀ {s t a b},
(⟨ swap , s ⟩ ==> t) ->
(s x = a /\ s y = b) ->
(t x = b /\ t y = a) := by
intros s t a b swap_s_t xa_yb
simp_all [swap]
cases xa_yb; rename_i xa yb
cases swap_s_t
rename_i swap_1 swap_23
cases swap_23
rename_i swap_2 swap_3
cases swap_1
cases swap_2
cases swap_3
simp [aval, upd, *]
Lets try to prove that swap indeed correctly swaps the values of x and y.
How can we specify this correctness property as a theorem?
How can we prove that theorem?
theorem swap_swaps : ∀ {s t : State} {n m : Val},
s x = n -> s y = m -> (⟨ swap, s ⟩ ==> t) -> (t x = m) /\ (t y = n) := by
sorry
Instead of the cases we can prove a theorem that precisely characterizes what the "shape"
of output state of an assignment is:
-- @[simp]
theorem assign_step : ∀ {x a s t}, (⟨ x <~ a, s ⟩ ==> t) <-> (t = (s [x := aval a s])) := by
intros x a s t
apply Iff.intro
. case mp => intros xs; cases xs ; trivial
. case mpr => intros; simp_all [] ; apply BigStep.Assign
And now, we can tell lean to use that assign_step to "fill in" the intermediate
s1, s2 and s3 to complete the proof.
theorem swap_swaps' : ∀ {s t : State} {n m : Val},
s x = n -> s y = m -> (⟨ swap, s ⟩ ==> t) -> (t x = m) /\ (t y = n) := by
intros s t n m sxn sym swap_123
simp_all [swap]
cases swap_123; rename_i s1 swap_1 swap_23
cases swap_23; rename_i s2 swap_2 swap_3
simp_all [assign_step, aval, upd]
Well, that wasn't too bad. But lets try a more interesting example:.
Example: Summing the numbers from 0..n
Consider the following loop which sums up the values of the numbers from 0 to x
∀ {start finish a}, ⟨ sum_com, start ⟩ ==> finish -> start x = a -> finish y = sumTo a
start x = a finish y = sumTo a
def sumTo (n: Nat) : Nat :=
match n with
| 0 => 0
| n' + 1 => n' + sumTo n'
def sum_com : Com :=
-- {{ x = a }}
y <~ 0 ;;
-- {{ x = a /\ y = 0 }}
WHILE
-- {{ x <= a }}
0 << x
DO
-- {{ x <= a /\ 0 < x }}
y <~ y + x ;;
x <~ x - 1
END
-- {{ y = sum a }}
-- x = a, y = 0
-- x = a-1, y=a
-- x = a-2, y=a + a -1
-- x = a-3, y=a + a - 1 + a - 2
-- x = 0 , y= a + a-1 + a-2 + ... + 1
-- y = 1 + 2 + 3 + ... + a
How can we specify that this correctly sums up the numbers 0 + ... + n ?
def sum (n:Nat) : Nat :=
match n with
| 0 => 0
| n' + 1 => n + sum n'
-- A program! ------------------------------------------------------------
abbrev csum := y <~ y + x ;; x <~ x - 1
abbrev wsum := WHILE 0 << x DO csum END
abbrev imp_sum := "y" <~ 0 ;; wsum
theorem wsum_sum' : (⟨ wsum, s ⟩ ==> t) -> ((t "y") = s "y" + sum (s "x")) := by
sorry
-- intro wsum_s_t
-- generalize h : wsum = ws at wsum_s_t -- LEAN:ANF BUG
-- induction wsum_s_t <;> simp_all [wsum]
-- . case WhileFalse =>
-- cases h
-- rename_i c _ s bfalse left _
-- simp [<-left] at bfalse
-- simp_all [bval, aval, sum]
-- . case WhileTrue =>
-- cases h
-- rename_i b c s s1 t btrue c_s_s1 w_s1_t left right
-- simp [<-left] at btrue
-- sorry
theorem csum_sum : (⟨ csum, s ⟩ ==> t) -> ( (t "x" = s "x" - 1) /\ (t "y") = s "y" + s "x")
:= by
intros cs; cases cs; rename_i s1 st1 st2; simp_all [assign_step]
by_cases (x=y) <;> (simp_all [upd, aval]; try intros; contradiction)
theorem wsum_sum : (⟨ wsum, s ⟩ ==> t) -> ((t "y") = s "y" + sum (s "x")) := by
intros wsums
generalize h : wsum = ws at wsums -- LEAN:ANF BUG
induction wsums <;> try simp_all []
.case WhileFalse =>
cases h
rename_i b c s bfalse cond _
have x_eq_0 : s "x" = 0 := by
simp [<-cond, bval, aval] at bfalse
assumption
simp_all [sum]
.case WhileTrue =>
rename_i b csum s s1 s2 btrue c_step _ _ _
cases h
rename_i cond hr
have s1xy : s1 "x" = s "x" - 1 /\ s1 "y" = s "y" + s "x" := by
apply csum_sum; simp_all []
cases s1xy
have sum_x : sum (s "x") = s "x" + sum (s "x" - 1) := by
simp [<-cond, bval, aval] at btrue
generalize hx : s "x" = sx
cases sx <;> simp_all [sum]
simp_all [Nat.add_assoc]
theorem while_sum : (⟨ imp_sum, s ⟩ ==> t) -> t "y" = sum (s "x") := by
intros ws
cases ws
rename_i y0_step ws_step
cases y0_step
generalize h : upd s y (aval 0 s) = s0 at ws_step
have hyp : ((t "y") = s0 "y" + sum (s0 "x")) := by apply wsum_sum; simp_all [<-h]
have h0 : s0 "y" = 0 := by simp_all [<-h, upd, aval]
have s0_x : s0 "x" = s "x" := by simp_all [<-h, upd]
simp_all []
Yikes, that was like pulling teeth. Lets look at a better way, introduced by Robert Floyd, back in 1967 (using the same example!)
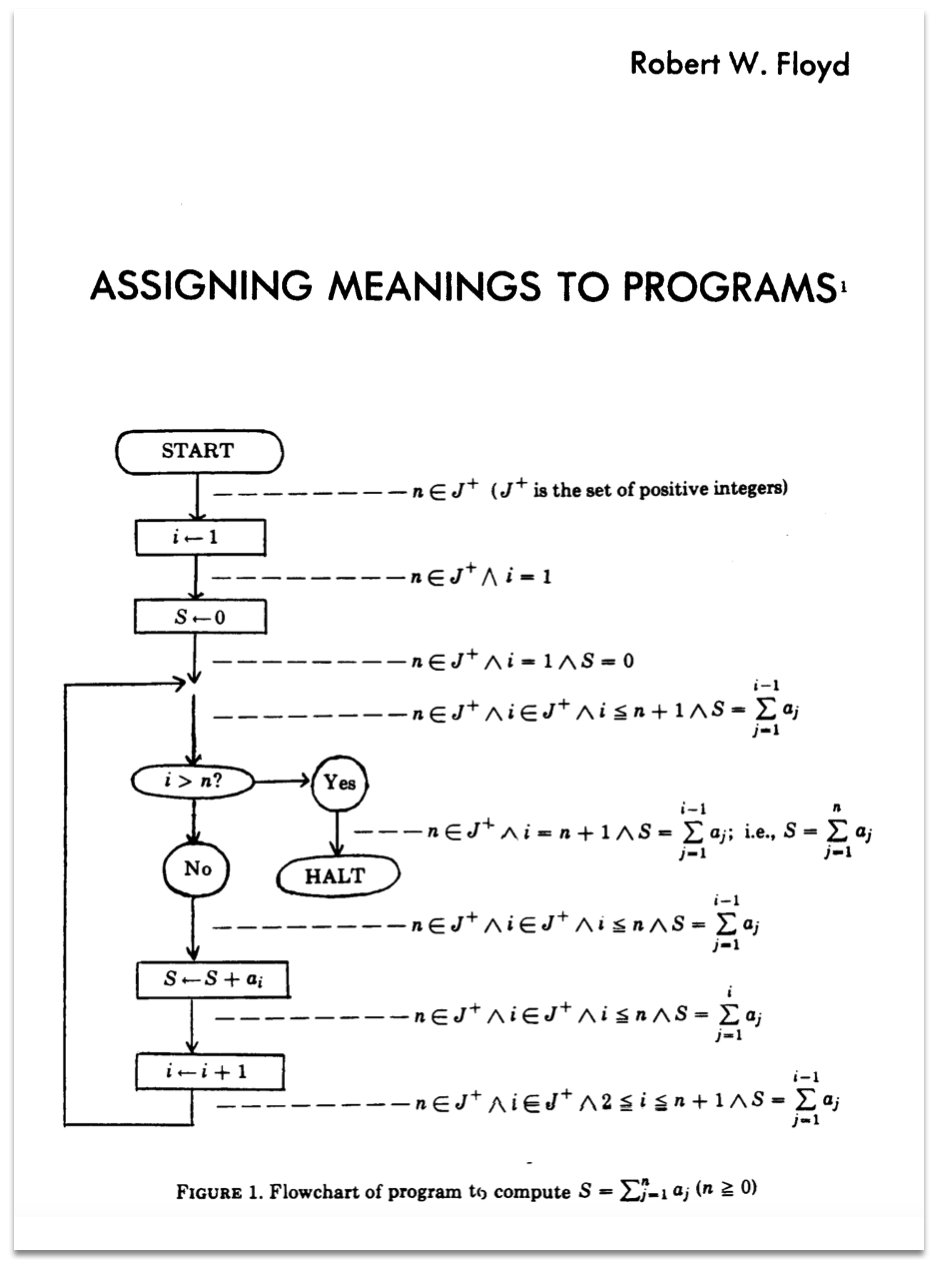
Floyd's paper formulated everything for flow-charts
In 1969 Tony Hoare reformulated those ideas as

which is what we today call axiomatic semantics or Floyd-Hoare (FH) Logic.
Assertions
The central idea in FH logic is the notion of an assertion which is simply property of a State,
that is some fact that is true (or not) about a particular program State.
abbrev Assertion := State -> Prop
For example, the state s defined as s0 [x := 10] [ y := 20] satisfies the following assertions
λ s -> s x < s yλ s -> s x + s y = 30
but does not satisfy the assertions
λ s -> s x = 0λ s -> s x > s y
Floyd-Hoare Triples
A Floyd-Hoare triple is a {{ p }} c {{ q }} where
pis a pre-condition assertion,cis a command, andqis a post-condition.
Intuitively, the triple {{ p }} c {{ q }} says that
If
- the command
cis executed from a state where the preconditionpholds and - the execution of
cterminates,
Then
- upon termination, the postcondition
qwill hold.
We can state the above precisely by defining when a triple is valid
@[simp]
def Valid (p: Assertion) (c: Com) (q: Assertion) :=
∀ s t, p s -> (⟨ c, s ⟩ ==> t) -> q t
notation:10 "⊧" " {{" p "}} " c " {{" q "}}" => Valid p c q
Example: Correctness of imp_sum
We can restate the correctness of imp_sum as a FH triple as
{ p } SKIP { p }
{ q [[ x := a ]] } x <~ a { q }
{ a > 15 } x <~ a { x > 15 }
example : ∀ {n},
⊧ {{ fun s => s "x" = n }} imp_sum {{ fun t => t "y" = sum n }}
:= by
simp_all []
intros n s t xn imp_step
simp_all [<-xn]
apply while_sum
trivial
Floyd-Hoare Logic
The notion of a valid triple is useful in defining a specification of correctness,
but we still have to go through the painful and quite tedious proof of while_sum to
actually verify the triple.
Proof Rules
The really clever contribution of Floyd and Hoare was to come up with a recipe comprising a system of proof rules that can be automatically applied to do the verification, without ever directly using the big-step semantics!
These rules are compositional meaning that we derive the triple {P} c {Q}
by using sub-derivations on the sub-commands of c.
Rule: Skip
For example, we have a rule for the Skip command that says
---------------- [skip]
⊢ {P} SKIP {P}
That is, for any assertion p we can derive that if p holds before the SKIP
then it must hold after as well.
Rule: Assign
⊢ { y > 0 } x <~ y { x > 0 }
⊢ { λ s => s y > 0 } x <~ y { λ s => (s x > 0) }
{ λ s => q (s [ x := (aval y s) ]) } x <~ y { q }
--------------------------------------- [assign]
⊢ { q [[ x := a ]] } x <~ a { q }
Rule: Sequence
The rule for sequencing two commands c1; c2 says that
⊢ {p} c1 {tmp} ⊢ {tmp} c2 {q}
⊢ {p} c1; c2 {q}
⊢ {p} c1 {q} ⊢ {q} c2 {r}
--------------------------------[seq]
⊢ {p} c1; c2 {r}
That is, ⊢ {p} c1; c2 {r} holds if
- there is some intermediate assertion
q - that holds after executing
c1from a{p}state, and c2then takes allqstates torstates.
Rule: Assignment
The rule for assignment is quite tricky.
When can we be sure that some assertion q holds after executing x <~ a ?
Lets look at some examples to build up some intuition.
What assertion can you write for ??? in each of the below?
-
{???} x <~ 10 { x > 0 } -
{???} x <~ y { x > 0 } -
{???} x <~ a+b { x + a > 0 }
Can you spot some sort of a pattern?
Indeed, if we want q to be true after the assignment x <~ a then
-
The only change made by the assignment is to
x -
So it must be that
qis true before the assignment -
Except with all occurences of
x(inq) replaced witha!
----------------------------- [ assign]
{ q [ x := a ] } x <~ a { q }
Example: Swap
Lets see how the rules for assignment and sequence work for our swap example from above.
{{ s y = b /\ s x = a }}
z <~ var x ;;
{{ s y = b /\ s z = a }}
x <~ var y ;;
{{ s x = b /\ s z = a }}
y <~ var z
{{ s x = b /\ s y = a }}
Rule: If-Then-Else
Lets try to work out the rule for establishing
a triple ⊢ {p} IF cond THEN c1 ELSE c2 {q}.
Lets think about this triple:
{ TRUE }
IF 0 < x
THEN y <~ x
ELSE y <~ 0 - x
{ 0 <= y }
What must be true before the IF-THEN-ELSE
so that we can be sure that 0 <= y after?
How can we know that the above triple holds?
Can you think of the appropriate triples that
must hold for c1 and c2 ? How about the rule
⊢ {P} c1 {Q} ⊢ {P} c2 {Q}
-------------------------------- [If?]
⊢ {P} IF b THEN c1 ELSE c2 {Q}
Is it "sound" (does it prove invalid triples ?)
Is it "complete" (does it prevent proving valid triples?)
How can we fix the rule?
⊢ {???} c1 {Q} ⊢ { ??? } c2 {Q}
------------------------------------ [If]
⊢ {P} IF b THEN c1 ELSE c2 {Q}
Lets go back to the example
⊢ {true /\ 0 < x} y <~ x { 0 <= y } ⊢ {true /\ ¬ 0 < x} y <~ 0 - x { 0 <= y }
-------------------------------------------------------------------------------- [If]
⊢ { true } IF (0 < x) THEN y <~ x ELSE y <~ 0 - x) { 0 <= y }
FH rules are too "tight"
Consider this triple: surely it should be valid but we cannot prove it with our rules :-(
{x = 10} SKIP { x > 0} (ex1)
The skip rule will let us prove that
⊢ {x=10} SKIP {x=10}
and that
⊢ {x > 0} SKIP {x > 0}
but surely we should also be able to prove {x=10} SKIP {x>0}?
Here's another example.
{x = 0} x <~ x + 1 {x = 1} (ex2)
The Assign rule will let us prove that {x+1 = 1} x <~ x + 1 {x = 1} but
not directly that {x=0} x <~ x + 1 {x=1} ... which seems silly!
Can you think about why the above triples ex1 and ex2 hold?
Bonus Rule: Consequence
How can we encode the above intuition as a rule?
We can relax the FH rules with the rule of consequence shown below.
∀ s. P(s) => P'(s) ⊢ {P'} c {Q'} ∀ s. Q'(s) => Q(s)
----------------------------------------------------------- [Consequence]
⊢ {P} c {Q}
This rule says that
- if you can establish the triple
⊢ {P'} c {Q'}then

- you can strengthen the precondition meaning, that if
⊢ {P'} c {Q'}holds then you can replace theP'with any assertionPthat is stronger thanP'i.e. wheneverPis true,P'is also true, and
- you can weaken the postcondition meaning, that if
⊢ {P'} c {Q'}holds then you can replace theQ'with any assertionQthat is weaker thanQ'i.e. wheneverQ'is true, thenQis also true.

So, for example, we can do
--------------------[skip]
⊢ {x=10} SKIP {x=10} x=10 => x>0
---------------------------------------------[conseq]
⊢ {x=10} SKIP {x>0}
------------------[skip]
x=10 => x>0 ⊢ {x>0} SKIP {x>0}
--------------------------------------------[conseq]
⊢ {x=10} SKIP {x>0}
--------------------------[assign]
x=0 => x+1=1 ⊢ {x+1=1} x <~ x + 1 {x=1}
---------------------------------------------[conseq]
⊢ {x=0} x <~ x + 1 {x=1}
Rule: While
Did we forget something: what about WHILE loops?
Lets pick a simple example. How can we prove that after executing the loop below,
the value of x is non-negative?
{{ True }}
⊆
{{ 1000 <= 1000 && 0 <= 0 }}
i <~ 0;
{{ 1000 <= 1000 && 0 <= i }}
x <~ 1000;
{{ 1000 <= x && 0 <= i }}
WHILE (i <= n) DO
{{ 1000 <= x && 0 <= i }}
⊆
{{ 1000 <= x+i && 0 <= i+1 }}
x <~ x + i;;
{{ 1000 <= x && 0 <= i+1 }}
i <~ i + 1
{{ 1000 <= x && 0 <= i }}
DONE
{{ 1000 <= x }}
Loop Invariants We need a way to describe an assertion that is true, no matter how many times the loop runs. Such an assertion is called a loop invariant. As the name suggests, the invariant must be true
- base case before the loop starts executing,
- inductive case if the invariant holds before one iteration, it must hold after an iteration.
Lets try to fill in the blanks in the rule below!
⊢ {???} c {???}
-------------------------------- [while]
⊢ {???} WHILE b DO c DONE {???}
When we're done, we should be able to prove (what is the magic I) ?
{true} i <~ 0;; x <~ 0;; WHILE i <= n DO (x <~ x+i;;i<~ i-1) DONE {0<=x}`
Example: sum
{{ x = i /\ 0 <= i }}
=>
{{ 0 + sum x = sum i /\ 0 <= i }}
y <~ 0
{{ y + sum x = sum i /\ 0 <= i}}
WHILE (0 < x) DO
{{ y + sum x = sum i /\ 0 <= x }}
y <~ y + x
x <~ x - 1
{{ ¬ 0 < x /\ y + sum x = sum i /\ 0 <= x }}
=>
{{ y = sum i}}
Formalizing the Floyd-Hoare Rules
It is pretty straightforward to formalize the FH rules
as an inductive predicate in lean.
Formalizing Implication ⊆
First, we need to define implication
open Com
@[simp]
def Implies (p q : Assertion) := ∀ s, p s -> q s
notation:10 p " ⊆ " q => Implies p q
Let us define the assertions tt ("true") and ff ("false") as
@[simp]
def tt : Assertion := fun _ => True
@[simp]
def ff : Assertion := fun _ => False
Now, we can easily prove the following implications, e.g.
theorem p_imp_true : ∀ {p : Assertion}, p ⊆ tt := by
simp []
theorem false_imp_p : ∀ {p : Assertion}, ff ⊆ p := by
simp []
example : (λ s => s x = 10) ⊆ (λ s => s x > 0 ) := by
intros s x_10
simp_all []
Formalizing Substitution
Next, lets formalize the idea of "substitution" as appears in the Assign rule.
⊢ { Q[x := a] } x <~ a { Q }
What, exactly, does it mean for Q to hold with the value of x replaced by a ?
notation:10 q "[[ " x ":=" a "]]" => fun s => q (s [ x := (aval a s) ])
Lets go and revisit our examples from above:
NOTE The funext s tactic lets us prove two functions are equal by proving
they produce the same (equal) result on all inputs s.
-- 1. `{true} x <~ 10 { 0 < x }`
example : ((λ s => 0 < s x) [[ x := 10 ]]) = tt := by
funext
simp [aval, upd]
-- 2. `{0 < y} x <~ y {0 < x}`
example : ((λ s => 0 < s x) [[ x := var y ]]) = (λ s => 0 < s y) := by
funext
simp [aval, upd]
theorem implies_refl : ∀ p, p ⊆ p := by
intro p s h
assumption
Formalizing The Proof Rules
inductive FH : Assertion -> Com -> Assertion -> Prop where
| Skip : ∀ {p},
FH p Skip p
| Assign : ∀ {p x a},
FH (p [[ x := a ]]) (x <~ a) p
| Seq : ∀ {p c1 c2 q r},
FH p c1 q -> FH q c2 r ->
FH p (c1 ;; c2) r
| If : ∀ {p b c1 c2 q},
FH (fun s => p s /\ bval b s) c1 q -> FH (fun s => p s /\ ¬ bval b s) c2 q ->
FH p (If b c1 c2) q
| While : ∀ {p b c},
FH (fun s => p s /\ bval b s) c p ->
FH p (While b c) (fun s => p s /\ ¬ bval b s)
| CnsL : ∀ {p' p c q},
FH p c q ->
(p' ⊆ p) ->
FH p' c q
| CnsR : ∀ {p c q q'},
FH p c q ->
(q ⊆ q') ->
FH p c q'
notation:10 "⊢" " {{" p "}} " c " {{" q "}}" => FH p c q
Examples, Mechanized
Swap
Recall the informal proof of swap above
{{ y = b /\ x = a }} p
z <~ var x ;;
{{ y = b /\ z = a }} p0
x <~ var y ;;
{{ x = b /\ z = a }} p1
y <~ var z
{{ x = b /\ y = a }} q
Lets formally prove the above using the FH rules. (Yuck, still gross!)
theorem swap_correct : ∀ {a b : Val},
⊢ {{ λ s => (s y = b /\ s x = a) }}
swap
{{ λ s => (s x = b /\ s y = a) }}
:= by
intros a b
generalize hp : (λ (s: State) => (s y = b /\ s x = a)) = p
generalize hp0 : (λ (s: State) => (s y = b /\ s z = a)) = p0
generalize hp1 : (λ (s: State) => (s x = b /\ s z = a)) = p1
generalize hq : (λ (s: State) => (s x = b /\ s y = a)) = q
have s0 : ⊢ {{ p }} z <~ var x {{ p0 }} := by
simp [<-hp, <-hp0]
apply FH.CnsL; apply FH.Assign; simp [aval,upd]
have s1 : ⊢ {{ p0 }} x <~ var y {{ p1 }} := by
simp [<-hp0, <-hp1]
apply FH.CnsL; apply FH.Assign; simp [aval,upd]
have s2 : ⊢ {{ p1 }} y <~ var z {{ q }} := by
simp [<-hp1, <-hq]; apply FH.CnsL; apply FH.Assign; simp [aval,upd]
simp [swap]
constructor
assumption
constructor
assumption
assumption
Loop
Recall the informal proof of loop above
{{ True }}
i <~ 0;
x <~ 0;
WHILE (i <= n) DO
x <~ x + i;;
i <~ i - 1
DONE
{{ 0 <= x }}
EXERCISE: Formally prove the above using the FH rules.
Sum
Finally,
{{ x = i /\ 0 <= i }}
=>
{{ 0 + sum x = sum i /\ 0 <= i }}
y <~ 0
{{ y + sum x = sum i /\ 0 <= i}}
WHILE (0 < x) DO
{{ y + sum x = sum i /\ 0 <= x }}
y <~ y + x
x <~ x - 1
{{ ¬ 0 < x /\ y + sum x = sum i /\ 0 <= x }}
=>
{{ y = sum i}}
def wsum_inv (i:Nat) : Assertion := λ s => s "y" + sum (s "x") = sum i
theorem y0_fh : ⊢ {{λ s => s x = i }} (y <~ 0) {{wsum_inv i }} := by
generalize h' : (λ (s:State) => s x = i) = p'
generalize h : (wsum_inv i [[ y := 0 ]]) = p
have aa : p' ⊆ p := by simp_all [<-h', <-h, Implies, wsum_inv, upd, aval]
have bb : ⊢ {{ p }} (y <~ 0) {{wsum_inv i }} := by simp [<-h]; apply FH.Assign
apply FH.CnsL
assumption
assumption
theorem csum_fh : ⊢ {{λ s => wsum_inv i s /\ (bval (0 << "x") s)}} csum {{wsum_inv i }} := by
generalize h1 : (wsum_inv i [[ x := x - 1 ]]) = q1
generalize h2 : (q1 [[ y := y + x ]]) = q2
have c1 : ⊢ {{ q1 }} x <~ x - 1 {{wsum_inv i }} := by simp_all [<-h1]; apply FH.Assign
have c2 : ⊢ {{ q2 }} y <~ y + x {{ q1 }} := by simp_all [<-h2]; apply FH.Assign
have c12 : ⊢ {{ q2 }} csum {{wsum_inv i }} := by apply FH.Seq; assumption; assumption
have imp1 : (λ s => wsum_inv i s /\ 0 < s x ) ⊆ q2 := by
simp_all [<-h2, <-h1, upd, Implies, bval, aval, wsum_inv]
by_cases (x = y) <;> simp_all []
.case neg =>
intros s h1 h2
generalize hx : s x = sx
cases sx <;> simp_all [sum, Nat.add_assoc]
apply FH.CnsL
apply c12
simp_all [bval, aval]
theorem imp_sum_fh : ⊢ {{ λ s => s "x" = i }} imp_sum {{ λ s => s "y" = sum i }} := by
have wsum_fh : ⊢ {{wsum_inv i }} wsum {{ λs => wsum_inv i s /\ ¬ (bval (0 << x) s) }} := by
apply FH.While; apply csum_fh
have imp_sum' : ⊢ {{ λ s => s "x" = i }} imp_sum {{ λ s => wsum_inv i s /\ ¬ (bval (0 << "x") s)}} := by
apply FH.Seq; apply y0_fh; apply wsum_fh
have wsum_exit : (λ s => wsum_inv i s /\ ¬ (bval (0 << "x") s)) ⊆ (λ s => s "y" = sum i) := by
simp_all [wsum_inv, Implies, bval, aval, sum]; intros; simp_all [sum]
apply FH.CnsR
apply imp_sum'
apply wsum_exit
Soundness of Floyd-Hoare Logic
The great thing about formalizing the definition of Validity and the proof rules
is that we can now prove that we did not just make stuff up.
That is, we can prove that the Floyd-Hoare logic is sound meaning that if we
can only derive valid triples in the logic. That is, if the proof rules let us
conclude the triple ⊢ {{p}} c {{q}} then that triple is in fact valid.
theorem fh_sound : ( ⊢ {{ p }} c {{ q }} ) -> ( ⊧ {{ p }} c {{ q }} ) := by
sorry
To recap: the Floyd-Hoare rules give us a sound way to construct proofs of programs, but, lets be honest, the construction is a real PITA.
Next, lets see how to dramatically automate these proofs using verification conditions.